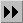Singular Manual: Global orderings

For all these orderings, we have Loc =

lp:: lexicographical ordering:
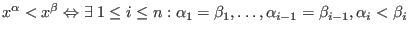$x^\alpha < x^\beta \Leftrightarrow \exists\; 1 \le i \le n : \alpha_1 = \beta_1, \ldots, \alpha_{i-1} = \beta_{i-1}, \alpha_i < \beta_i$ .
rp:: inverse lexicographical ordering:
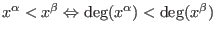
$x^\alpha < x^\beta \Leftrightarrow \exists\; 1 \le i \le n : \alpha_n = \beta_n, \ldots, \alpha_{i+1} = \beta_{i+1}, \alpha_i < \beta_i.$
dp:: degree reverse lexicographical ordering:
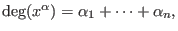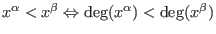let $\deg(x^\alpha) = \alpha_1 + \cdots + \alpha_n,$ then $x^\alpha < x^\beta \Leftrightarrow \deg(x^\alpha) < \deg(x^\beta)$ or
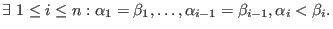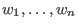
$\deg(x^\alpha) = \deg(x^\beta)$ and $\exists\ 1 \le i \le n: \alpha_n = \beta_n, \ldots, \alpha_{i+1} = \beta_{i+1}, \alpha_i > \beta_i.$
Dp:: degree lexicographical ordering:
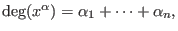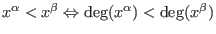let $\deg(x^\alpha) = \alpha_1 + \cdots + \alpha_n,$ then $x^\alpha < x^\beta \Leftrightarrow \deg(x^\alpha) < \deg(x^\beta)$ or
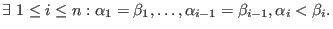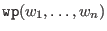
$\deg(x^\alpha) = \deg(x^\beta)$ and $\exists\ 1 \le i \le n:\alpha_1 = \beta_1, \ldots, \alpha_{i-1} = \beta_{i-1}, \alpha_i < \beta_i.$
wp:: weighted reverse lexicographical ordering:
let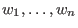 $w_1, \ldots, w_n$ be positive integers. Then 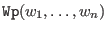${\tt wp}(w_1, \ldots, w_n)$ is defined as dp but with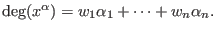 $\deg(x^\alpha) = w_1 \alpha_1 + \cdots + w_n\alpha_n.$
Wp:: weighted lexicographical ordering:
let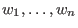 $w_1, \ldots, w_n$ be positive integers. Then 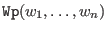${\tt Wp}(w_1, \ldots, w_n)$ is defined as Dp but with $\deg(x^\alpha) = w_1 \alpha_1 + \cdots + w_n\alpha_n.$

User manual for Singular version 4.4.1, 2025, generated by texi2html.