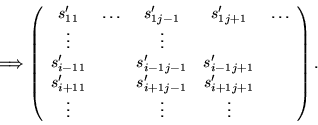2.1 The common algorithm

The common algorithm stores the reduction process of a standard basis computation and obtains in this way a basis for the module of syzygies. Assume that an R-module 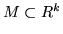$M\subset R^k$ is given by the columns of a matrix:

$$A= \left( \begin{array}{cccc} a_{11} &a_{12} &\ldots &a_{1... ...\vdots\\ a_{n1} &a_{n2} &\ldots &a_{nn} \end{array} \right)$$

Then we add a new module component to each element of the given basis. The extra component then notices what happens with its corresponding element:

$$\left( \begin{array}{ccccc} &&&&\\ &&&&\\ &&A&&\\ &&&... ...C'&\\ &&&&&\vert&&&\\ &&&&&\vert&&& \end{array} \right) .$$

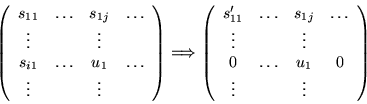
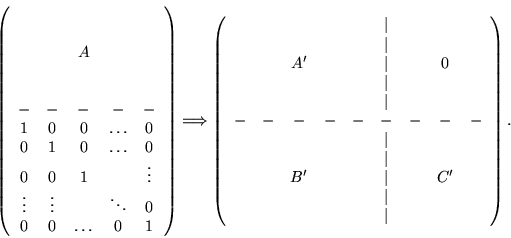
After a standard basis computation we obtain a matrix like the right one, where A' corresponds to the standard basis of A, B' is a transformation matrix, i.e., A'=A*B' and C' represents a basis of the module syzygies of A. In fact, every syzygy constitutes a certain way to obtain 0 as linear combination of the given generators. In this way, we find a basis of all syzygies. Otherwise a syzygy, which is not included, will produce elements with new leading terms.

Following this idea we obtain an easy implementation of this algoritm:

W := Syz$(\bf S)$
INPUT: S, a basis of an ideal
OUTPUT: S' a minimal set of generators; W' the module of syzygies of S'

$W:= \emptyset$
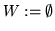
T := initSyz (S)
T' := std (S)
setRegularity(T')
WHILE 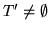$T' \not= \emptyset$ DO

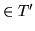IF t$\in T'$ is syzygy W := $W\cup \{$t$\}$
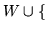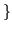
T' := $T'\setminus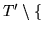\{$t$\}$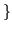

END
(S',W') := minimize(S,W).

T := initSyz$(\bf S)$
INPUT: S, a standard basis $v_1, \ldots, v_s$
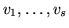
OUTPUT: T, the set $[v_1, 1, 0, \ldots, 0], \ldots, [v_s, 0, \ldots, 0,1]$

i := r; $T := \emptyset$
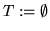
S := interReduce(S)
WHILE 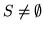$S \not= \emptyset$ DO

s := the first element from S
i := i+1
$S := S \backslash \{s\}$
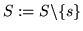
s := s + e_i
$T := T \cup \{s\}$

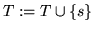
END
setSyzygyOrder(r)

$(\bf W',S') :=$ minimize$(\bf W,S)$
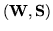
INPUT: S, a basis, W, its syzygies
OUTPUT: S', a minimal system of generators, W', its syzygies

W' := W
S' := S
WHILE searchUnit(W',i,j) DO

W' := Gauss(W',i,j)
S' := $S'\setminus\{s_i\}$

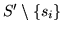
END

In the interreduction we subtract multiples of elements from others as long as any leading term divides another one. The interreduction of the input must always precede the adding of new module components. Otherwise this would result in a much more complicated structure of the module of syzygies.

In the part of minimization one searches for units of the ground ring in the entres of the matrix C' corresponding to the syzygies. Then one performs a Gaussian elimination with the associated row and cancels the row and the column where the unit was found at the end:

$$\left( \begin{array}{cccc} s_{11}&\ldots&s_{1j} &\ldots\\ ... ... 0 &\ldots&u_1 & 0 \\ \vdots& &\vdots & \end{array} \right)$$

$$\Longrightarrow \left( \begin{array}{ccccc} s'_{11} &\ldot... ...1 j+1}& \\ \vdots & &\vdots &\vdots & \end{array} \right) .$$

Notice that for each Gaussian elimination one has to multiply all remaining columns with the unit u₁ which implies that the length of all polynomials grows at least by the number l₁=length(u₁) of monomials of u₁. In the case of global computaions all units are just constants. However, for local or mixed orderings these units are polynomials in the non global variables and the length of the polynomials grows during n Gaussian elemenations by:

$$l_1^nl_2^{n-1}\ldots l_{n-1}^2l_n,$$

where l_i=length(u_i) is the number of monomials in the i-th unit at the begin of the minimization. To decrease this growth one might use Bareiss' algorithm, but this would imply additional polynomial divisions.

Our experience agrees with this observation: in a non-global case it is often the minimization which is the really hard part to compute a minimal resolution, whereas in the global case it is always the standard basis.