


Next: 2. Block type Bruhat
Up: Splitting algorithm for vector
Previous: Splitting algorithm for vector
1. Introduction and notation
Let
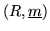 be either a complete local Noetherian commutative algebra over a field K
or a graded K-algebra
be either a complete local Noetherian commutative algebra over a field K
or a graded K-algebra
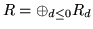 ,
R0=K and
,
R0=K and
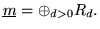 Let
Let
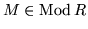 be a finitely generated (or graded resp.) R-module.
In the local case it is known (cf. [Yo]) that the module M is
indecomposable if and only if the endomorphism ring
be a finitely generated (or graded resp.) R-module.
In the local case it is known (cf. [Yo]) that the module M is
indecomposable if and only if the endomorphism ring
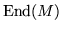 is local.
But this criteria is difficult
to handle, since it involves usage of non-commutative methods. Here we
present several versions of a criteria based on a presentation matrix of
M, which may be checked using only the Groebner-basis algorithm in
various forms.
The algorithm has several applications:
is local.
But this criteria is difficult
to handle, since it involves usage of non-commutative methods. Here we
present several versions of a criteria based on a presentation matrix of
M, which may be checked using only the Groebner-basis algorithm in
various forms.
The algorithm has several applications:
- (i1) Let R be the graded coordinate ring of a projective K-variety
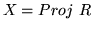 ,
let V be a vector bundle on X with
,
let V be a vector bundle on X with
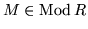 an associated graded R-module.
The algorithm produces the direct sum decomposition of V.
an associated graded R-module.
The algorithm produces the direct sum decomposition of V.
- (i2) More general, let
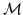 be a coherent sheaf on X. We can decide
wether
be a coherent sheaf on X. We can decide
wether 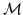 is indecomposable.
is indecomposable.
- (i3) Let R be the local ring of an isolated hypersurface
singularity X defined by a polynomial equation
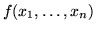 .
If X is a suspension over X0, i.e.
.
If X is a suspension over X0, i.e.
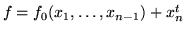 and
f0 an equation of X0,
there is a useful theorem (cf. [HP] (2.8)) connecting maximal
Cohen-Macaulay-modules (MCM) over X and X0 and generalizing
Knörrer's periodicity theorem.
and
f0 an equation of X0,
there is a useful theorem (cf. [HP] (2.8)) connecting maximal
Cohen-Macaulay-modules (MCM) over X and X0 and generalizing
Knörrer's periodicity theorem.
THEOREM
If
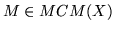 and
Ri:=R/xni+1R,
and
Ri:=R/xni+1R,
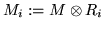 then
then
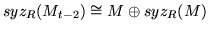 and Mt-2 is a
deformation of M0 over Rt-2.
and Mt-2 is a
deformation of M0 over Rt-2.
Knowing
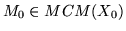 we obtain MCM's over R by computing
infinitesimal deformations of M0 and then inspecting the direct
summands of their R-syzygy-module. In this way computations are
partially done for X0 an Ak-singularity (cf. [MPP]),
which has stimulated the development of the algorithm.
Our algorithm is used for the verification of the indecomposability
of the module constructed there.
we obtain MCM's over R by computing
infinitesimal deformations of M0 and then inspecting the direct
summands of their R-syzygy-module. In this way computations are
partially done for X0 an Ak-singularity (cf. [MPP]),
which has stimulated the development of the algorithm.
Our algorithm is used for the verification of the indecomposability
of the module constructed there.
Throughout this paper we restrict the notation to the local case.
The graded case is handled analogously.
First we will fix some notation. A module M may be presented by matrices
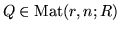



Next: 2. Block type Bruhat
Up: Splitting algorithm for vector
Previous: Splitting algorithm for vector
| ZCA Home |
Reports |
![]()