| Example |
Felsch |
HLT |
NONE |
P-ALL |
P-G |
P-R |
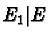 |
98 |
695 |
157 |
572 |
572 |
572 |
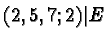 |
216 |
224 |
143 |
276 |
276 |
275 |
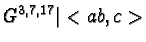 |
724 |
1381 |
1153 |
968 |
1576 |
2206 |
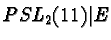 |
660 |
661 |
660 |
947 |
888 |
897 |
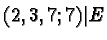 |
1221 |
2286 |
1534 |
1561 |
1518 |
2613 |
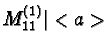 |
720 |
721 |
720 |
720 |
720 |
720 |
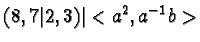 |
824 |
1241 |
973 |
1862 |
1759 |
1325 |
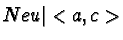 |
2650 |
4553 |
1683 |
3828 |
2699 |
3361 |
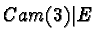 |
653 |
2189 |
161 |
1884 |
1884 |
1883 |
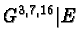 |
21504 |
69990 |
75058 |
59350 |
59338 |
62715 |
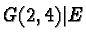 |
3188 |
2973 |
467 |
2767 |
2767 |
2585 |
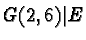 |
7889 |
4194 |
1343 |
4746 |
4746 |
3904 |
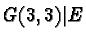 |
25481 |
29007 |
9753 |
76022 |
76022 |
69897 |
|