5. Orderings

As will be seen later, orderings play an important rôle for the enumeration process. The strategies presented will behave differently when they are combined with different orderings. Three different orderings are defined which are well-founded, total, and admissible. They are implemented in MRC 1.2 and are used for the coset enumerations.

Definition 1 (Length-Lexicographical Ordering)  
Let $\Sigma$ be a finite alphabet. Let $>$ be a total precedence on $\Sigma$. Let $v \equiv v_1\ldots v_n \in \Sigma^{*}, v_i \in \Sigma, w \equiv w_1\ldots w_m \in \Sigma^{*}, w_j \in \Sigma$. The length-lexicographical ordering $\succ_{ll}$ is defined as:

$v \succ_{ll} w$	iff	$\vert v\vert > \vert w\vert$ or
		$(\vert v\vert = \vert w\vert$ and $\exists\; 1 \leq i \leq n: (v_i > w_i \wedge \forall\; 1 \leq j < i: v_j \equiv w_j))$

Definition 2 (Knuth-Bendix Ordering)  
Let $\Sigma$ be a finite alphabet. Let $>$ be a total precedence on $\Sigma$. Let $v \equiv v_1\ldots v_n \in \Sigma^{*}, v_i \in \Sigma, w \equiv w_1\ldots w_m \in \Sigma^{*}, w_j \in \Sigma$. Let $g: \Sigma \rightarrow \mathbb {N}$ be a total function attaching a weight to each letter of the alphabet. Then $g$ is defined on words as:

$$\begin{eqnarray*} g: & \Sigma^{*} & \rightarrow \mathbb {N}\\ & u & \mapsto \sum_{i=1}^{\vert u\vert} g(u_i) \end{eqnarray*}$$

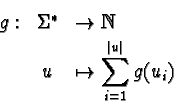
The Knuth-Bendix ordering (kbo) $\succ_{kbo}$ is defined as:

$v \succ_{kbo} w$	iff	$g(v) > g(w)$ or
		$(g(v) = g(w)$ and $\exists\; 1 \leq i \leq n: (v_i > w_i \wedge \forall\; 1 < j \leq i: v_j \equiv w_j))$

Definition 3 (Syllable Ordering)  
Let $\Sigma$ be a finite alphabet. Let $>$ be a total precedence on $\Sigma$. Let $\tau: \Sigma \rightarrow \{l, r\}$ be a total function named status function. Let $\max(u), u \in \Sigma^{*}$ be the largest letter of $u$ with respect to the precedence on $\Sigma$.

The syllable ordering $\succ_{syl, \tau}$ is defined as:

$v \succ_{syl, \tau} w$ iff $\vert v\vert _{\max(vw)} > \vert w\vert _{\max(vw)}$ or

		$[$ $\max(vw) = a$ and $\vert v\vert _a = \vert w\vert _a = n$ and 

		 		$v \equiv v_1av_2a \ldots v_nav_{n+1}$ and                                    $w \equiv w_1aw_2a \ldots w_naw_{n+1}$ and 

		 		$[$ $\tau(a) = r$ and 

		 		 		 $\exists\; 1 \leq i \leq n+1: (v_i \succ_{syl, \tau} w_i \wedge \forall\; i+1 \leq j \leq n+1: v_j \equiv w_j]$ or 

		 		$[$ $\tau(a) = l$ and 

		 		 		 $\exists\; 1 \leq i \leq n+1: (v_i \succ_{syl, \tau} w_i \wedge \forall\; 1 \leq j \leq i-1: v_j \equiv w_j]]$

Notice, that the syllable ordering has a recursive definition. In MRC 1.2 the orderings are implemented according to the definitions given with the restriction that for the syllable ordering $\forall\; a \in \Sigma: \tau(a) = l$ or $\forall\; a \in \Sigma: \tau(a) = r$. That is, for all letters of the alphabet syllables are either compared from left to right or from right to left.

The comparison of terms is frequently needed for example for the determination of the head term after each reduction step. Therefore, the time needed to compare two terms with respect to the chosen ordering directly influences the time needed to compute the prefix Gröbner basis. As can be seen from the definitions, the length-lexicographical ordering has at least to compare the length of the two terms and at most compare the length and compare each character of the terms. The Knuth-Bendix ordering has at least to compute the sum of both terms and at most compute the sum and compare each character of the term. The syllable ordering has at least to count the number of syllables of each term and at most in addition compare the syllables recursively. Thus, we have that the expense needed for the comparison of two terms grows from length-lexicographical over Knuth-Bendix to syllable orderings.