Bibliography

Adams and Loustaunou1994

Adams, W.W.; Loustaunou, P. (1994). An Introduction to Gröbner Bases. AMS Graduate Studies in Mathematics 3, Providence, R.I.

Apel1998

Apel, J. (1998). Computational Ideal Theory in Finitely Generated Extension Rings. Preprint, Leipzig.

Apel and Klaus1991

Apel, J.; Klaus, U. (1991). FELIX -- an assistant for algebrists, in Proc. ISSAC'91, 382-389.

Arnold, Gusein-Zade and Varchenko1985

Arnold, V.I.; Gusein-Zade, S.M., Varchenko, A.N. (1995). Singularities of Differential Maps, Volume I. Birkhäuser.

D. Bayer1982

Bayer, D. (1982). The Division Algorithm and the Hilbert-Scheme. Thesis, Harvard University, Cambridge, MA.

D. Bayer and Stilman1982-1990

Bayer, D.; Stillman, M. (1982 - 1990). Macaulay: A system for computation in algebraic geometry and commutative algebra. Available via ftp from zariski.harvard.edu.

T. Bayer2000

Bayer, T. (2000). Computation of moduli spaces for semiquasihomogeneous singularities and an implementation in SINGULAR. Diplomarbeit, Kaiserslautern.

Becker and Wörmann1996

Becker, E.; Wörmann, T. (1996). Radical computations of zero-dimensional ideals and real root counting. Mathematics and Computers in Simulation 42, 561-569.

Becker and Weispfennig1993

Becker, T.; Weispfennig, V. (1993). Gröbner Bases, A Computational Approach to commutative Algebra. Graduate Texts in Mathematics 141, Springer.

Brieskorn1970

Brieskorn, E. (1970). Die Monodromie der isolierten Singularitäten von Hyperflächen. Manuscripta Math. 2, 103-161.

Buchberger1965

Buchberger, B. (1965). Ein Algorithmus zum Auffinden der Basiselemente des Restklassenringes nach einem nulldimensionalen Polynomideal. PhD Thesis, University of Innsbruck, Austria.

Buchberger1970

Buchberger, B. (1970). Ein algorithmisches Kriterium für die Lösbarkeit eines algebraischen Gleichungssystems. Äqu. Math. 4, 374-383.

Buchberger1985

Buchberger, B. (1985). Gröbner bases: An algorithmic method in polynomial ideal theory. Recent trends in multidimensional system theory, N.B. Bose, Ed., Reidel.

Buchberger and Winkler1998

Buchberger, B.; Winkler, F. (ed.) (1998). Gröbner Bases and Applications. LNS 251, 109-143. CUP.

Canny and Emiris1997

Canny, J.F.; Emiris, I.Z. (1997). A Subdivision-Based Algorithm for the Sparse Resultant. Preprint, Berkeley.

Cohen, Cuypers and Sterk1999

Cohen, A. M.; Cuypers, H; Sterk, H. (Eds.) (1999). Some Tapas of Computer Algebra. Springer Verlag.

Cox, Little and O'Shea1992

Cox, D.; Little, J.; O'Shea, D. (1992). Ideals, Varieties and Algorithms. Springer Verlag.

Cox, Little and O'Shea1998

Cox, D.; Little, J.; O'Shea, D. (1998). Using Algebraic Geometry. Springer Verlag.

Capani, Niesi and Robbiano1995

Capani, A.; Niesi, G.; Robbiano, L.: CoCoA (1995). Available via http://lancelot.dima.unige.it

Davenport, Siret and Tournier1988

Davenport, J.H.; Siret, Y.; Tournier, E. (1988). Computer Algebra. Systems and Algorithms for Algebraic Computations, 2nd ed., Academic Press.

Decker, Greuel and Pfister1998

Decker, W.; Greuel, G.-M.; Pfister, G. (1998). Primary Decomposition: Algorithms and Comparisons. In: Greuel, G.-M.; Matzat, H.B.; Hiss, G. (Eds.), Algorithmic Algebra and Number Theory 187-220. Springer Verlag, Heidelberg.

Decker, Greuel, De Jong and Pfister1998

Decker, W.; Greuel, G.-M.; De Jong, T.; Pfister, G. (1998). The normalisation: a new Algorithm, Implementation and Comparisons. Proc. Computational Methods for Representations of Groups and Algebras, 177-185, Birkhäuser.

Decker, Ein and Schreyer1993

Decker, W.; Ein, L.; Schreyer, F.-O. (1993). Construction of Surfaces in 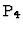$\P _4$. J. Algebraic Geometry 2, 185-237.

Decker and De Jong1998

Decker, W.; De Jong, T. (1998). Gröbner Bases and Invariant Theory. In: B. Buchberger and F. Winkler (Eds.): Gröbner Bases and Applications. LNS 251, 61-89. CUP.

Derksen1997

Derksen, H. (1997). Constructive Invariant Theory and the Linearization Problem, Thesis, Basel.

Eisenbud1993

Eisenbud, D. (1993). Open Problems in Computational Algebraic Geometry and Commutative Algebra. In: Eisenbud, D.; Robbiano, L. (Eds.): Computational Algebraic Geometry and Commutative Algebra, Cortona 1991, Cambridge University Press, Cambridge, England, 49-71.

Eisenbud1995

Eisenbud, D. (1995). Commutative Algebra with a view toward Algebraic Geometry. Springer Verlag.

Eisenbud, Diaconis and Sturmfels1996

Eisenbud, D., Diaconis, P.; Sturmfels, B. (1996). Lattice walks and primary decomposition. To appear in the Rotafest Proceedings.

Eisenbud, Huneke and Vasconcelos1992

Eisenbud, D.; Huneke, C.; Vasconcelos, W. (1992). Direct methods for primary decomposition. Invent. Math. 110, 207-235.

Eisenbud, Peeva and Sturmfels

Eisenbud, D.; Peeva, I.; Sturmfels, B.: Noncommutative Gröbner Bases for Commutative Ideals. To appear in Proc. Am. Math. Soc..

Eisenbud and Sturmfels1996

Eisenbud, D.; Sturmfels, B. (1996). Binomial ideals. Duke Math. J. 84, 1-45.

Fröberg1997

Fröberg, R. (1997). An introduction to Gröbner Bases, John Wiley & Sons.

Frühbis-Krüger2000

Frühbis-Krüger, A. (2000). Construction of Moduli Spaces for Space Curve Singularities of Multiplicity 3. Preprint, Kaiserslautern.

Gatermann1999

Gatermann, K. (1999). Computer Algebra Methods for Equivariant Dynamical systems. Preprint SC 99-26, Berlin.

Von zur Gathen and Gerhard1999

Von zur Gathen, J.; Gerhard, J. (1999). Modern Computer Algebra, Cambridge University Press.

Gelfand, Kapranov and Zelevinksi1994

Gelfand, I.; Kapranov, M.; Zelevinski, A. (1994). Discriminants, Resultants and Multidimensional Determinants. Birkhäuser Verlag.

Gerard and Levelt1973

Gerard, R., Levelt, A.H.M. (1973). Invariants mesurant l'irregularite en un point singulier des systemes de'equations differentielles lineares, Ann. Inst. Fourier Grenoble 23, 157-195.

Gianni and Trager1997

Gianni, P.; Trager, B. (1997). Integral closure of noetherian rings. Proceedings ISSAC 97.

Gianni, Trager and Zacharias1988

Gianni, P.; Trager, B.; Zacharias, G. (1988). Gröbner Bases and Primary Decomposition of Polynomial Ideals. J. Symbolic Computation 6, 149-167.

Grabmeier, Kaltofen and Weispfennig2000

Grabmeier,J.; Kaltofen, E.; Weispfennig V. (2000). Handbook of Computer Algebra, Foundations, Applications, Systems. To be published by Springer Verlag.

Gräbe,1995

Gräbe, H.-G.: (1995). Algorithms in local algebra. J. Symb. Comp. 19, 545-557

Grassmann et al1994

Grassmann, H.; Greuel, G.-M.; Martin, B.; Neumann, W.; Pfister, G.; Pohl, W.; Schönemann, H.; Siebert, T. (1994). Standard bases, syzygies and their implementation in SINGULAR. Beiträge zur angewandten Analysis und Informatik, Shaker, Aachen, 69-96.

Grauert and Remmert1971

Grauert, H.; Remmert, R. (1971). Analytische Stellenalgebren. Springer Verlag.

Grayson and Stillmann1996

Grayson, D.; Stillmann, M. (1996): Macaulay2, a computer software system designed to support research in commutative algebra and algebraic geometry. Available from http://math.uiuc.edu/Macaulay2.

Greuel1975

Greuel, G.-M. (1975). Der Gauss-Manin Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten. Math. Ann. 214, 235-266.

Greuel1992

Greuel, G.-M. (1992). Deformation und Klassifikation von Singularitäten und Moduln. Jahresber. Deutsch. Math.-Verein. Jubiläumstagung 1990, 177-238.

Greuel1986

Greuel, G-M. (1986). Constant Milnor number implies constant multiplicity for quasihomogeneous singularities. Manuscripta Math. 56, 159-166.

Greuel and Kröning1990

Greuel, G.-M.; Kröning, H. (1990). Simple Singularities in Positive Characteristic. Math. Z. 203, 339-354.

Greuel, Lossen and Shustin1998

Greuel, G.-M.; Lossen, C.; Shustin, E. (1998). Plane curves of minimal degree with prescribed singularities. Invent. Math. 133, 539-580.

Greuel, Martin and Pfister1985

Greuel, G.-M.; Martin, B.; Pfister, G. (1985). Numerische Charakterisierung quasihomogener Gorenstein-Kurvensingularitäten. Math. Nachr. 124, 123-131.

Greuel and Pfister1996

Greuel, G.-M.; Pfister,G. (1996). Advances and improvements in the theory of standard bases and syzygies. Arch. Math. 66, 163-1796.

Greuel and Pfister1998

Greuel, G.-M.; Pfister, G. (1998). Gröbner bases and algebraic geometry. In: B. Buchberger and F. Winkler (Eds.): Gröbner Bases and Applications. LNS 251, 109-143. CUP.

Greuel, Pfister and Schönemann1990-1998

Greuel, G.-M.; Pfister, G.; Schönemann, H. (1990-1998). Singular, A System for Polynomial Computations, version 1.2 User Manual. In: Reports On Computer Algebra, number 21. Centre for Computer Algebra, University of Kaiserslautern, June 1998. Available via http://www.mathematik.uni-kl.de/~zca/Singular.

Hillebrand1999

Hillebrand, D. (1999). Triangulierung nulldimensionaler Ideale -- Implementierung und Vergleich zweier Algorithmen. Diplomarbeit, Dortmund.

Hironaka1964

Hironaka, H. (1964). Resolution of singularities of an algebraic variety over a field of characteristic zero. Ann. of Math. 79, 109-326.

ISSAC1988-1998

ISSAC (1988-1998). International Symposium on Symbolic and Algebraic Computation, Proceedings.

De Jong1998

De Jong, T. (1998). An algorithm for computing the integral closure. J. Symb. Comp. 26, 273-277.

Kalkbrenner1994

Kalkbrenner, M. (1994). Prime decomposition of radicals in polynomial rings. J. Symb. Comp. 18, 365-372.

Kalkbrenner1998

Kalkbrenner, M. (1998). Algorithmic Properties of Polynomial Rings. J. Symb. Comp. 26, 525-581.

Kemper1996

Kemper, G. (1996). Calculating Invariant Rings of Finite Groups over Arbitrary Fields. J. Symb. Comp. 21, 351-366.

Kontsevich and Manin1994

Kontsevich, M; Manin, Y. (1994). Gromov-Witten classes, quantum cohomology, and enumerative Geometry. Comm. Math. Phys. 164, 525-562.

Krick and Logar1991

Krick, T.; Logar, A. (1991). An algorithm for the computation of the radical of an ideal in the ring of polynomials. AAECC9, Springer LNCS 539, 195-205.

Krüger1997

Krüger, K. (1997). Klassifikation von Hyperflächensingularitäten. Diplomarbeit, Kaiserslautern.

Lamm1999

Lamm, M. (1999). Hamburger-Noether-Entwicklung von Kurvensingularitäten. Diplomarbeit, Kaiserslautern.

Lossen1999

Lossen, C. (1999). New Asymptotics for the Existence of Plane Curves with Prescribed Singularities. Comm. in Alg. 27, 3263-3282.

Laudal1979

Laudal, A. (1979). Formal moduli of algebraic structures. SLN 754. Springer Verlag.

Martin1998

Martin, B. (1998). Computing versal deformations with SINGULAR. In: Matzat, B.H.; Greuel, G.-M.; Hiss, G. (Eds.), Algorithmic Algebra and Number Theory, 283-294, Springer Verlag, Heidelberg.

Martin, Pfister1989

Martin, B.; Pfister, G. (1989). The kernel of the Kodaira-Spencer map of the versal 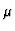$\mu$-constant deformation of an irreducible plane curve singularity with 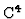${\mathbb{C}}^4$-action. J. Symbolic Computation, 7, 527-539.

Martin1996

Martin, B. (1996). Computing Massey products using SINGULAR. Preprint M-02, Cottbus.

Matzat, Greuel and Hiss1998

Matzat, B.H.; Greuel, G.-M.; Hiss, G. (Eds.) (1998). Algorithmic Algebra and Number Theory, 187-220, Springer Verlag, Heidelberg.

Mishra1993

Mishra, B. (1993). Algorithmic Algebra, Texts and Monographs in Computer Science, Springer.

Möller1998

Möller, H.M. (1998). Gröbner Bases and Numerical Analysis. In: B. Buchberger and F. Winkler (Eds.): Gröbner Bases and Applications. LNS 251, 159-178. CUP.

Mora1982

Mora, T. (1982). An algorithm to compute the equations of tangent cones. Proc. EUROCAM 82, Lecture Notes in Computer Science.

Mora1989

Mora, T. (1989). Gröbner Bases in Non-Commutative Algebras. LNCS 358, 150-161, Springer Verlag.

Mora, Pfister, Traverso1992

Mora, T.; Pfister, G.; Traverso, C. (1992). An Introduction to the Tangent Cone Algorithm. Advances in Computing Research, issued in Robotics and non-linear geometry, (6), 199-270.

O'Shea1987

O'Shea, D. (1987). Topologically trivial deformations of isolated quasihomogeneous hypersurface singularities are equimultiple. Proc. AMS 101, 260-262.

Pfister1991

Pfister, G. (1991). The tangent cone algorithm and some applications to algebraic geometry. Proceedings of the MEGA Conference 1990, Birkhäuser (94).

Pfister and Schönemann1989

Pfister, G.; Schönemann, H. (1989). Singularities with exact Poincarè complex but not quasihomogeneous. Revista Mathematica Madrid (2) 2y3 161-171.

Ritt1950

Ritt, J.F. (1950). Differential Algebra. Colloquium Publications Vol. 33, AMS, New York.

Saito1971

Saito, K.: Quasihomogene isolierte Singularitäten von Hyperflächen. Invent. Math. 14, 123-142.

Saito, Sturmfels and Takayama1999

Saito, M.; Sturmfels, B.; Takayama, N. (1999). Gröbner Deformations of Hypergeometric Differential Equations. Springer Verlag.

Seidenberg1975

Seidenberg, A. (1975). Construction of the integral closure of a finite integral domain II. Proc. Amer. Math. Soc. 52, 368-372.

Schreyer1980

Schreyer, F.-O. (1980). Die Berechnung von Syzygien mit dem verallgemeinerten Weierstrass'schen Divisionssatz. Diplomarbeit, Hamburg.

Schreyer

Schreyer, F.-O. (1991). A standard basis approach to syzygies of canonical curves. J. reine angew. Math. 421, 83-123.

Schreyer1986

Schreyer, F.-O. (1986). Syzygies of canonical curves and special linear series. Math. Ann. 275.

Schulze1999

Schulze, M. (1999). Computation of the Monodromy of an Isolated Hypersurface Singularity, Diploma Thesis, Kaiserslautern.

Shimoyama and Yokoyama1996

Shimoyama, T.; Yokoyama, K. (1996). Localization and Primary Decomposition of Polynomial ideals. J. Symb. Comp. 22, 247-277.

Stolzenberg1968

Stolzenberg, G. (1968). Constructive normalization of an algebraic variety. Bull. Amer. Math. Soc. 74, 595-599.

Sturmfels1993

Sturmfels, B. (1993). Algorithms in Invariant Theory. Springer Verlag.

Ufnarovski1998

Ufnarovski, V. (1998). Introduction to Noncommutative Gröbner Bases Theory. In: B. Buchberger and F. Winkler (Eds.): Gröbner Bases and Applications. LNS 251, 259-280. CUP.

Vasconcelos1991

Vasconcelos, V.W. (1991). Computing the integral closure of an affine domain. Proc. AMS 113 (3), 633-638.

Vasconcelos1998

Vasconcelos, V.W. (1998). Computational Methods in Commutative Algebra and Algebraic Geometry, Springer Verlag.

Verschelde1999

Verschelde, J. (1999). Polynomial homotopies for dense, sparse and determinantal systems. Preprint Math.NA/9907060.

Wall1983

Wall, C.T.C. (1983). Classification of unimodal isolated singularities of complete intersections. In: Singularities, Arcata 1981 (Ed. Orlik, P.). Proc. Sympos. Pure Math. 40(2), 625-640.

Wang1992

Wang, D. (1992). Irreducible Decomposition of Algebraic Varieties via Characteristic Sets and Gröbner Bases. Computer Aided Geometric Design 9, 471-484.

Wenk1999

Wenk, M. (1999). Resultantenmethoden zur Lösung algebraischer Gleichungssysteme implementiert in SINGULAR. Diplomarbeit, Kaiserslautern.

Zariski1971

Zariski, O. (1971). Some open questions in the theory of singularities. Bull. AMS, 481-491.