A (complex) singularity is, by definition, nothing but a complex
analytic germ ![]() together with its analytic local ring
together with its analytic local ring
![]() ,
where
,
where
![]() is the convergent power series ring in
is the convergent power series ring in
![]() .
For an arbitrary field
.
For an arbitrary field ![]() let
let
![]() for some ideal
for some ideal ![]() in the formal power series ring
in the formal power series ring ![]() . We call
. We call
![]() Spec
Spec![]() or
just
or
just ![]() a singularity (
a singularity (
![]() denotes the maximal ideal of the local ring
denotes the maximal ideal of the local ring ![]() )
and write
)
and write
![]() for the convergent and for the formal power
series ring if the statements hold for both.
for the convergent and for the formal power
series ring if the statements hold for both.
If
![]() is an ideal with
is an ideal with
![]() then the singularity of
then the singularity of ![]() at
at ![]() is,
using the above notation,
is,
using the above notation,
![]() .
However, we may also consider the local ring
.
However, we may also consider the local ring
![]() with
with
![]() the localisation of
the localisation of
![]() at
at
![]() , as the singularity of
, as the singularity of ![]() at 0.
Geometrically, for
at 0.
Geometrically, for
![]() , the difference is the following:
, the difference is the following:
![]() describes the variety
describes the variety ![]() in an arbitrary small neighbourhood of
0 in the Euclidean topology while
in an arbitrary small neighbourhood of
0 in the Euclidean topology while
![]() describes
describes ![]() in an arbitrary small
neighbourhood of 0 in the (much coarser) Zariski topology.
in an arbitrary small
neighbourhood of 0 in the (much coarser) Zariski topology.
At the moment, we can compute efficiently only in
![]() as we shall explain below. In many cases of interest, we are happy
since invariants of
as we shall explain below. In many cases of interest, we are happy
since invariants of ![]() at 0 can be computed in
at 0 can be computed in
![]() as well as in
as well as in
![]() . There are, however, others (such as
factorisation), which are completely different in both rings.
. There are, however, others (such as
factorisation), which are completely different in both rings.
![]() is called non-singular or regular or smooth if
is called non-singular or regular or smooth if
![]() is isomorphic (as local ring) to a power series ring
is isomorphic (as local ring) to a power series ring
![]() , or if
, or if
![]() is a regular local ring.
is a regular local ring.
By the implicit function theorem, or by the Jacobian criterion, this is
equivalent to the fact that ![]() has a system of generators
has a system of generators
![]() such that the Jacobian matrix of
such that the Jacobian matrix of
![]() has rank
has rank ![]() in some neighbourhood of 0.
in some neighbourhood of 0. ![]() is called an isolated singularity
if there is a neighbourhood
is called an isolated singularity
if there is a neighbourhood ![]() of 0 such that
of 0 such that
![]() is regular everywhere.
is regular everywhere.
In order to compute with singularities, we need the notion of standard basis which is a generalisation of the notion of Gröbner basis, cf. GP1,GP2.
A monomial ordering is a total order on the set of monomials
![]() satisfying
satisfying
Any
![]() can be written uniquely as
can be written uniquely as
![]() , with
, with
![]() and
and
![]() for any
non-zero term
for any
non-zero term
![]() of
of ![]() . We set lm
. We set lm
![]() , the leading monomial of
, the leading monomial of ![]() and
lc
and
lc![]() , the leading coefficient of
, the leading coefficient of
![]() .
.
For a subset
![]() we define the leading ideal of
we define the leading ideal of ![]() as
as
So far, the general case is not different to the case of a well-ordering. However, the following definition provides something new for non-global orderings:
For a monomial ordering ![]() define the multiplicatively closed set
define the multiplicatively closed set
![$\displaystyle \,K[x] := S^{-1}_> K[x] = \{\dfrac{f}{u} \;\vert\; f \in K[x], u \in
S_>\},
$](img213.gif)
Note that
![]() Loc
Loc![]() and
Loc
and
Loc![]() if and only if
if and only if ![]() is global and
Loc
is global and
Loc![]() if and only if
if and only if ![]() is local (which justifies the names).
is local (which justifies the names).
Let ![]() be a fixed monomial ordering. In order to have a short
notation, I write
be a fixed monomial ordering. In order to have a short
notation, I write
Let
![]() be an ideal. A finite set
be an ideal. A finite set
![]() is
called a standard basis of
is
called a standard basis of ![]() if and only if
if and only if
![]() , that
is, for any
, that
is, for any
![]() there exists a
there exists a ![]() satisfying
lm
satisfying
lm![]() lm
lm![]() .
.
If the ordering is a well-ordering, then a standard basis ![]() is
called a Gröbner basis. In this case
is
called a Gröbner basis. In this case ![]() and, hence,
and, hence,
![]() .
.
Standard bases can be computed in the same way as Gröbner bases except that we need a different normal form. This was first noticed by Mo for local orderings (called tangent cone orderings by Mora) and, in general, by GP1,Getal.
Let
![]() denote the set of all finite and ordered subsets
denote the set of all finite and ordered subsets
![]() .
A map
.
A map
NF is called a weak normal form if, instead of (ii), only the following condition (ii') holds:
Moreover, we need (in particular for computing syzygies) (weak) normal forms
with standard representation: if
![]() , we can
write
, we can
write
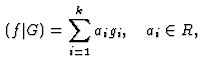
Indeed, if ![]() and
and ![]() consist of polynomials, we can compute, in finitely
many steps, weak normal forms with standard representation such that
consist of polynomials, we can compute, in finitely
many steps, weak normal forms with standard representation such that ![]() and
NF
and
NF![]() are polynomials and, hence, compute polynomial standard bases which
enjoy most of the properties of Gröbner bases.
are polynomials and, hence, compute polynomial standard bases which
enjoy most of the properties of Gröbner bases.
Once we have a weak normal form with standard representation, the general standard basis algorithm may be formalised as follows:
STANDARDBASIS(G,NF) [arbitrary monomial ordering]
Input: ![]() a finite and ordered set of polynomials, NF a
weak normal form with standard representation.
a finite and ordered set of polynomials, NF a
weak normal form with standard representation.
Output: ![]() a finite set of polynomials which is a standard
basis of
a finite set of polynomials which is a standard
basis of
![]() .
.
- ![]() ;
;
-
![]() ;
;
- while
![]()
choose
![]() ;
;
![]() ;
;
![]() NF
NF![]() spoly
spoly![]() ;
;
if
![]()
![]() ;
;
![]() ;
;
- return ![]() ;
;
Here spoly
![]() denotes the
denotes the
![]() -polynomial of
-polynomial of ![]() and
and ![]() where
where
![]() lm
lm![]() lm
lm![]() .
.
The algorithm terminates by Dickson's lemma or by the noetherian property of the polynomial ring (and since NF terminates). It is correct by Buchberger's criterion, which generalises to non-well-orderings.
If we use Buchberger's normal form below, in the case of a well-ordering, STANDARDBASIS ist just Buchberger's algorithm:
NFBUCHBERGER(f,G) [well-ordering]
Input: ![]() a finite ordered set of polynomials,
a finite ordered set of polynomials, ![]() a
polynomial.
a
polynomial.
Output: ![]() a normal form of
a normal form of ![]() with respect to
with respect to ![]() with
standard representation.
with
standard representation.
- ![]() ;
;
- while
![]() and exist
and exist ![]() so that
lm
so that
lm![]() lm
lm![]()
choose any such ![]() ;
;
![]() spoly
spoly![]() ;
;
- return ![]() ;
;
For an algorithm to compute a weak normal form in the case of an arbitrary ordering, we refer to GP1.
To illustrate the difference between local and global orderings, we compute the dimension of a variety at a point and the (global) dimension of the variety.
The dimension of the singularity ![]() , or the dimension of
, or the dimension of ![]() at
0, is, by definition, the Krull dimension of the analytic local ring
at
0, is, by definition, the Krull dimension of the analytic local ring
![]() , which is the same as the Krull dimension
of the algebraic local ring
, which is the same as the Krull dimension
of the algebraic local ring
![]() in case
in case
![]() is generated by polynomials, which follows easily from the
theory of dimensions by Hilbert-Samuel series.
is generated by polynomials, which follows easily from the
theory of dimensions by Hilbert-Samuel series.
Using this fact, we can compute ![]() by computing a standard basis of
the ideal
by computing a standard basis of
the ideal
![]() generated in
Loc
generated in
Loc![]() with respect to any
local monomial ordering on
with respect to any
local monomial ordering on ![]() . The dimension is equal to the
dimension of the corresponding monomial ideal (which is a combinatorial
problem).
. The dimension is equal to the
dimension of the corresponding monomial ideal (which is a combinatorial
problem).
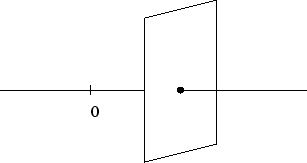
For example, the dimension of the affine variety
![]() is 2 but
the dimension of the singularity
is 2 but
the dimension of the singularity ![]() (that is, the dimension of
(that is, the dimension of ![]() at the
point 0) is 1:
at the
point 0) is 1:
Using SINGULAR we compute first the global dimension with the degree reverse
lexicographical ordering denoted by dp and then the local dimension at 0
using the negative degree reverse lexicographical ordering denoted by ds.
Note that in the local ring
![]() (represented by
the ordering ds)
(represented by
the ordering ds) ![]() is a unit.
is a unit.
ring R = 0,(x,y,z),dp; //global ring ideal i = yx-y,zx-z; ideal si = groebner(i); si; ==> si[1]=xz-z, //leading ideal of i is <xz,xy> ==> si[2]=xy-y dim(si); ==> 2 //global dimension = dim R/<xz,xy> ring r = 0,(x,y,z),ds; //local ring ideal i = yx-y,zx-z; ideal si = groebner(i); si; ==> si[1]=y //leading ideal of i is <y,z> ==> si[2]=z dim(si); ==> 1 //local dimension = dim r/<y,z>