Monodromy and Gauß-Manin connection

The monodromy of a morphism $f : X \rightarrow S$ between complex spaces or algebraic schemes/$\mathbf{C}$, which we suppose to be a differentiable fibre bundle outside the discriminant $\Delta \subset S$, describes the action of the fundamental group of $S \setminus \Delta$ on the cohomology $H^\ast(X_t, \mathbf{C})$ of the general fibre. The Gauß-Manin connection may be considered as an algebraic description of the monodromy action by means of differential forms. Finally, the mixed Hodge structure is an analytic structure on $H^\ast(X_t, \mathbf{C})$ generalising the Hodge decomposition of compact, smooth algebraic varieties. These concepts have many applications and were widely studied in the global situation for proper maps as well as in the local situation for isolated singularities, for a survey see [Ku]. Here we shall only consider the local case.

Let $f \in \langle x\rangle \subset \mathbf{C}\{x_0, \dots, x_n\}$ be a convergent power series (in practice a polynomial) with isolated singularity at 0 and $\mu = \dim_\mathbf{C}\mathbf{C}\{x\}/\langle f_{x_0}, \dots, f_{x_n}\rangle$ the Milnor number of $f$. Then $f$ defines in an $\varepsilon$-ball $B_\varepsilon$ around 0 a holomorphic function $f :B_\varepsilon \rightarrow \mathbf{C}$, and, by a theorem of Milnor, there exists a small $\delta$-disc $S_\delta$ in $\mathbf{C}$ around $0$ such that $f : B_\varepsilon \setminus X_0 \rightarrow S_\delta \setminus \{0\}$ is a $C^\infty$-fibre bundle so that the general fibre $X_t = f^{-1} (t)$, $t \not= 0$, is homotopy equivalent to a bouquet of $\mu$ $n$-dimensional spheres.

The simple, counterclockwise path $\gamma$ in $S_\delta$ around $0$ induces a $C^\infty$-diffeomorphism of $X_t$ ($t \not= 0$) and an automorphism $T$ of the singular cohomology group $H^n(X_t, \mathbf{C})$ which is a $\mu$-dimensional $\mathbf{C}$-vector space. The automorphism $T$ is called the local Picard-Lefschetz monodromy of $f$. We address the problem of computing the eigenvalues and the Jordan normal form of $T$.

The first important theorem is the monodromy theorem, due to Deligne in the global and to Brieskorn in the local situation which says that the eigenvalues of $T$ are roots of unity, that is, we have $T = e^{2\pi i M}$, where $M$ is a complex matrix with eigenvalues in $\mathbf{Q}$.

Hence, we are left with the problem of computing the eigenvalues and the Jordan normal form of $M$. Since $X_t$ is a complex Stein manifold, its complex cohomology can be computed, via the holomorphic de Rham theorem, by using holomorphic differential forms, which is the starting point of Brieskorn's algorithm for computing the monodromy. To cut a long story short, we just mention that the Brieskorn lattices (cf. [Br])

$$H' = \Omega^n/\left(df \wedge \Omega^{n-1} + d \Omega^{n-1}\r... ...\quad H^{\prime\prime} = \Omega^{n+1}/df \wedge d \Omega^{n-1}$$

are free $\mathbf{C}\{t\}$-modules of rank $\mu$. Here $(\Omega,d)$ denotes the complex of holomorphic differential forms in $(\mathbf{C}^n,0)$. We define the local Gauß-Manin connection of $f$ as

$$\bigtriangledown : df \wedge H^\prime = df \wedge \Omega^n... ...{\prime\prime},\quad [df \wedge \omega]\longmapsto [d \omega].$$

Extending $\bigtriangledown$ to an endomorphism of $H'' \otimes_{\mathbf{C}\{t\}} \mathbf{C}(t)$ and describing it with respect to a basis, we see immediately that the kernel of $\bigtriangledown$, together with a basis of $H^{\prime\prime}$, is the same as the solutions of a rank $\mu$ system of ordinary differential equations

$$\frac{dy}{dt} = -Ay,\qquad A = (a_{ij})= \sum_{i \ge -p} A_i t^i \in \mbox{Mat}\bigl(\mu \times \mu, \mathbf{C}(t)\bigr),$$

in a neighbourhood of $0$ in $\mathbf{C}$. The connection matrix $A$ has a pole at $t = 0$ and is holomorphic for $t \not= 0$. If $\phi_t = (\phi_1, \dots, \phi_\mu)$ is a fundamental system of solutions at a point $t \not= 0$, then the analytic continuation of $\phi_t$ along the path $\gamma$ transforms $\phi_t$ into another fundamental system $\phi'_t$ which satisfies $\phi'_t = T_\bigtriangledown \phi_t$ for some matrix $T_\bigtriangledown \in \mbox{GL}(\mu, \mathbf{C})$.

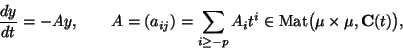
It is a fundamental fact that the Picard-Lefschetz monodromy $T$ coincides with the monodromy $T_\bigtriangledown$ of the Gauß-Manin connection.

Brieskorn [Br] used this fact to describe the essential steps for an algorithm to compute the characteristic polynomial of $T$. Results of Gerard and Levelt [GL] allowed the extension of this algorithm to compute the Jordan normal form of $T$. An implementation of Schulze in SINGULAR is able to compute interesting examples (including the uni- and bimodal singularities, [Sch]).

The algorithm uses the regularity theorem which says that there exists a basis of some lattice in $H^{\prime\prime} \otimes \mathbf{C}(t)$ such that the connection matrix $A$ has a pole of order 1.

Basically, if $A = A_{-1} t^{-1} + A_0 + A_1 t + \ldots$ has a simple pole, then $T = e^{2\pi i A_{-1}}$ is the monodromy (this holds if the eigenvalues of $A_{-1}$ do not differ by integers which can be achieved algorithmically).

SINGULAR example for computing the monodromy (omitting the output):

> LIB "mondromy.lib";
> ring R = 0,(x,y),ds;
> poly f = x2y2+x6+y6;     //example of A'Campo (monodromy is not
> matrix M = monodromy(f); //diagonalisable) 
> print(jordanform(M));    //prints Jordan normalform of monodromy

Ingredients for the implementation of Brieskorn's algorithm:

1. Computation of standard bases and normal forms for local orderings;
2. find $k$ so that $f^k \in \langle f_{x_0}, \dots, f_{x_n}\rangle$ and express $f^k$ as linear combination of $f_{x_0}, \dots, f_{x_n}$;
3. computation of the connection matrix on increasing lattices in $H^{\prime\prime} \otimes \mathbf{C}(t)$ up to sufficiently high order (until saturation) by linear algebra over $\mathbf{Q}$;
4. computation of the transformation matrix to a simple pole by linear algebra over $\mathbf{Q}$.

The most expensive parts are certain normal form computations for a local ordering and the linear algebra part because here one has to deal iteratively with matrices with several thousand rows and columns.

In the remaining part of this section we describe a new algorithm, developed by M. Schulze, based on the theory of $\mathcal{D}$-modules ( $\mathcal{D}=\mathbf{C}\{t\}[\partial_t ]$): the complex $\Omega[D]$ with differential $\mathbf{d}$ defined by

$$\mathbf{d}(\omega D^k):=d\omega D^k-df\wedge\omega D^{k+1}$$

is a complex of $\mathcal{D}$-modules with $\mathcal{D}$-action

$$\partial_t \omega D^k=\omega D^{k+1}\,,\qquad t\omega D^k=f\omega D^k-k\omega D^{k-1}.$$

The $\mathcal{D}$-module $\mathcal{H}:= H^{n+1}(\Omega[D],\mathbf{d})=\Omega^{n+1}[D]/\mathbf{d}\Omega^n[D]$ is called the Gauß-Manin system of $f$. The operator $\partial_t$ is invertible on $\mathcal{H}$. For $k\ge0$, let

$$F_k\Omega^{n+1}[D]:=\textstyle{\bigoplus\limits_{i=0}^k}\Omega^{n+1}D^i$$

and $F_k\mathcal{H}$ be the image of $F_k\Omega^{n+1}[D]$ under the canonical map $\Omega^{n+1}[D]\rightarrow\mathcal{H}$. This defines a filtration $F$ on $\mathcal{H}$ called the Hodge filtration. By the De Rham and Poincaré lemma, $df\wedge H'=\partial_t ^{-1} F_0\mathcal{H}\subset F_0\mathcal{H}=H''$. We denote by

$$\mathbf{C}\bigl\{\:\bigl\{\partial_t ^{-1} \bigr\}\:\bigr\}:... ...t\, \sum_{i\ge0}\frac{a_i}{i!}t^i\in\mathbf{C}\{t\}\biggr\}\,,$$

the ring of micro-differential operators with constant coefficients and abbreviate $s:=\partial_t ^{-1}$. Then $H''$ is a free $\mathbf{C}\{\{s\}\}$-module of rank $\mu$. By definition, $df\wedge\Omega^n\subset\Omega^{n+1}$ is isomorphic to the Jacobian ideal of $f$, and $\Omega_f=\Omega^{n+1}/df\wedge\Omega^n$ to the Milnor algebra. Using Gröbner basis methods, one can compute a monomial $\mathbf{C}$-basis $m=\{m_1,\dots,m_\mu\}$ of $\Omega_f$, inducing a section $v\in Hom_\mathbf{C}(\Omega_f,H'')$ of the projection $\pi$ and an isomorphism $\mathbf{C}\{\{s\}\}^\mu\cong H''$, by Nakayama's lemma. We define the matrix

$$B=\sum_{k\ge0}B_ks^k\in{Mat}\bigl(\mu\times \mu,\mathbf{C}\{\{s\}\}\bigr)$$

of multiplication by $t$ this respect to $m$, i.e., $Bm:=tm$. An easy computation shows that $B+s^2\partial_s$ is the basis representation of $t$ with respect to $m$.

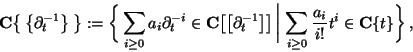
By definition of the differential $\mathbf{d}$, computing $B$ up to order $k-1$ amounts to expressing $k$ times an element of $\Omega^{n+1}$ in the basis $m$ and $df\wedge\Omega^n$, which is the Jacobian ideal of $f$. This can be done using Gröbner basis methods. To do the $k$-th step in the computation of the saturation $H''_\infty$ of $H''$, one has to compute $B$ up to order $k$. To compute the residue of $\partial_t$ on $H''_\infty$, whose eigenvalues are the eigenvalues of monodromy, one has to compute $B$ up to sufficiently high order and compute a $\mathbf{C}\{\{s\}\}$-basis of $H''_\infty$ as well as the basis representation of the images of this basis under $\partial_t t$ with respect to this basis. This can also be done using Gröbner basis methods.

Compared to the Brieskorn algorithm, we have interchanged the roles of $\partial_t ^{-1}$ and $t$. The $\partial_t ^{-1}$-structure of $H''$ is much more natural and there are many advantages of this new algorithm: There are no problems with estimations, no huge linear algebra problems, we need not to lift a power of $f$ in the Jacobian ideal, the basis of $H''$ is easier to compute, and so on. The main point is that we can continue the computation when we have to increase the order of $B$. In the Brieskorn algorithm, we have to start again almost from the beginning. Nevertheless, the three components of this new algorithm explained above also require difficult computations, especially the first one. The new algorithm can be extended to compute the Jordan normal form of the monodromy in a similar way as it was done in [Sch].

Problems:

1. Generalise the algorithm of M. Schulze to isolated complete intersection singularities.

2. Find an algorithm to compute the $V$-filtration of the mixed Hodge structure of an isolated hypersurface singularity.

3. Compute the spectrum, resp. the spectral pairs, of an isolated hypersurface singularity.

The last problem was solved (and implemented in SINGULAR) by S. Endraß for nondegenerate singularities. M. Schulze has made progress in attacking 2. and 3.