

Next: Symbolic-numerical polynomial solving
Up: Applications of Computer Algebra
Previous: Moduli spaces and invariants
It is a classical and interesting problem, which is still in the centre of
theoretical research, to study the variety
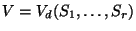 of
(irreducible) curves
of
(irreducible) curves
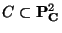 of degree
of degree 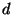 having exactly
having exactly 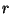 singularities of prescribed (topological or analytical) types
singularities of prescribed (topological or analytical) types
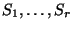 . Among the most important questions are:
. Among the most important questions are:
- Is
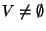 (existence problem)?
(existence problem)?
- Is
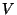 irreducible (irreducibility problem)?
irreducible (irreducibility problem)?
- Is
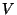 smooth of expected dimension (
smooth of expected dimension (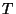 -smoothness problem)?
-smoothness problem)?
A complete answer is only known in the special case of nodal curves, that is,
for
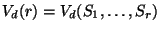 with
with 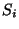 ordinary nodes
(
ordinary nodes
(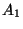 -singularities):
-singularities):
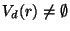 and
and 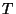 -smooth
-smooth
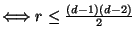 (Severi, 1921),
(Severi, 1921),
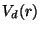 is irreducible (if
is irreducible (if
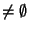 ) (Harris, 1985).
Even for cuspidal curves there is no sufficient and necessary answer
to any of the above questions and one can hardly expect such an answer.
) (Harris, 1985).
Even for cuspidal curves there is no sufficient and necessary answer
to any of the above questions and one can hardly expect such an answer.
Clearly, one can easily give an upper bound for the number of
singular points that may occur on a plane irreducible curve  of degree
of degree  :
by the genus formula
:
by the genus formula 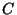 can have, at most,
can have, at most,
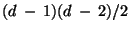 singularities. Another upper bound for the (weighted) number of singularities
arises from
applying Bézout's Theorem to the intersection of two generic polars of
singularities. Another upper bound for the (weighted) number of singularities
arises from
applying Bézout's Theorem to the intersection of two generic polars of 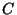 :
:
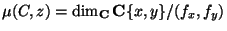 the Milnor number of
the Milnor number of 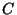 at
at 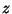 .
.
On the other hand, in the case of arbitrary topological types 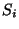 ,
we have the following existence theorem, which is asymptotically optimal (with
respect to the occurring invariants and the exponent of
,
we have the following existence theorem, which is asymptotically optimal (with
respect to the occurring invariants and the exponent of 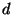 )
)
Theorem: [GLS,Lo].
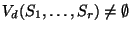 if
if
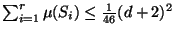 and two additional conditions for the five
``worst'' singularities hold true.
and two additional conditions for the five
``worst'' singularities hold true.
In case of only one singularity we have the slightly better sufficient
condition for existence,
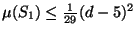 .
.
The theorem is just an existence statement, the proof gives
no hint how to produce any equation. To produce explicit equations one needs
some constructive method. Then the computer can be used in order to check the
construction, or even, to improve the results. The following is a prominent
example (actually, it belongs to a series of ``world record'' examples):
Example: [GN]
The irreducible curve with affine equation
has degree 65 and an 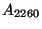 -singularity
-singularity
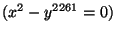 and a semiquasihomogeneous singularity
and a semiquasihomogeneous singularity 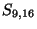 with principal part
with principal part
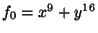 as only singularities. In particular, it is an element
of the variety
as only singularities. In particular, it is an element
of the variety
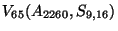 which has negative expected dimension (hence is not T-smooth).
which has negative expected dimension (hence is not T-smooth).
In order to verify this, one may proceed, using SINGULAR, as follows:
> ring s = 0,(x,y),ds;
> poly f = y2-2x28y-4x21y17+4x14y33-8x7y49+20y65+x56+4x49y16;
> matrix Hess = jacob(jacob(f)); //the Hessian matrix of f
> vdim(std(jacob(f))); //the Milnor number of f
2260
Since the rank of the Hessian at 0 is checked to be 1, 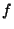 has an
has an 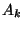 singularity at 0; it is an
singularity at 0; it is an 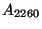 -singularity since the Milnor number is
2260. In the following we show that the projective curve defined by
-singularity since the Milnor number is
2260. In the following we show that the projective curve defined by 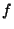 has no
further singularities in the affine part. This follows from
has no
further singularities in the affine part. This follows from
confirmed by SINGULAR:
> vdim(std(jacob(f)+f));
2260 // multiplicity of Sing(C) at 0 (local ordering)
> ring r = 0,(x,y),dp;
> poly f = fetch(s,f);
> vdim(std(jacob(f)+f));
2260 // multiplicity of Sing(C) (global ordering)
Finally, we have to consider the singularities at infinity:
> ring sh = 0,(x,y,z),dp;
> poly f = fetch(s,f);
> poly F = homog(f,z); F; // homogeneous polynomial defining C
4x49y16+20y65+x56z9-8x7y49z9+4x14y33z18-4x21y17z27-2x28yz36+y2z63
> ring r1 = 0,(y,z),dp;
> map phi = sh,1,y,z;
> poly g = phi(F); // F in affine chart (x=1)
> vdim(std(jacob(g)+g));
120
> ring r2 = 0,(y,z),ds; // local ring at (1:0:0)
> poly g = fetch(r1,g); g;
z9+4y16-2yz36-4y17z27+4y33z18-8y49z9+20y65+y2z63
> vdim(std(jacob(g)+g));
120
As before, we can conclude that there is precisely one singularity of 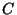 on
the line at infinity, situated at
on
the line at infinity, situated at 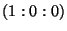 , being semiquasihomogeneous of type
, being semiquasihomogeneous of type
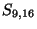 . (Note that in our computation we have considered all points at
infinity except
. (Note that in our computation we have considered all points at
infinity except 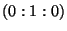 . The latter is obviously not a point of
. The latter is obviously not a point of 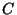 ).
).
In the following we should like to mention a few problems and conjectures
which are currently in the centre of research in connection with singular
curves in
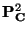 .
.
Computing zero-dimensional ideals
Many of the questions concerning plane projective curves with prescribed
singularities can be translated to properties of zero-dimensional
(homogeneous) ideals
![$I\subset \mathbf{C}[x,y,z]$](img184.gif) , e.g.,
, e.g.,
- existence of curves with (ordinary) multiple points in prescribed
position, or, more generally, existence of curves with prescribed
position of infinitely near points (clusters),
- T-smoothness of the varieties
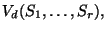
- existence of (global) deformations of projective curves.
For instance, consider the following problem: given points
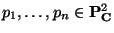 and positive integers
and positive integers
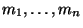 . Determine the dimension of the variety of
curves of any degree
. Determine the dimension of the variety of
curves of any degree 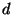 passing through each of the points
passing through each of the points 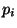 with
multiplicity
(at least)
with
multiplicity
(at least) 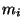 ,
, 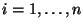 . The equivalent formulation would be: determine
the ideal
. The equivalent formulation would be: determine
the ideal
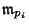 the maximal ideal at
the maximal ideal at 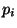 , and
compute the Hilbert function
, and
compute the Hilbert function 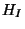 of I.
of I.
Harbourne-Hirschowitz conjecture: Let 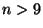 ,
,
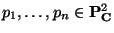 in general position,
in general position, 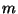 a positive integer, and let
a positive integer, and let
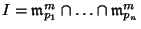 . Then the
Hilbert function satisfies
. Then the
Hilbert function satisfies
for all 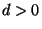 . In other words, the variety of curves with n singular points of
multiplicity (at least)
. In other words, the variety of curves with n singular points of
multiplicity (at least) 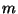 at the prescribed (generic) points has the
expected dimension.
at the prescribed (generic) points has the
expected dimension.
There are several special cases where this conjecture is known to hold true; in
particular, C. Ciliberto and R. Miranda [CM]
have proven that it always holds for
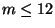 . Nevertheless the general conjecture is still far from being proven.
. Nevertheless the general conjecture is still far from being proven.
Nagata conjecture: Let 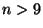 ,
,
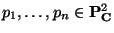 in
general position,
in
general position, 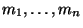 positive integers, and let
positive integers, and let
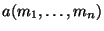 denote the minimal degree
of a curve passing through each of the points
denote the minimal degree
of a curve passing through each of the points 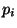 with multiplicity
(at least)
with multiplicity
(at least) 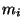 ,
, 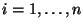 . Then
. Then
N. Nagata [Na] has proven the statement to be true for any 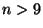 being
a square. There are many people working to prove this conjecture for other
integers
being
a square. There are many people working to prove this conjecture for other
integers 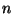 ([Ra]), or, at least, to improve the known lower bounds for
([Ra]), or, at least, to improve the known lower bounds for
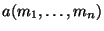 (the best known general bound is probably given in
[Ro]). But the general question is still widely open.
(the best known general bound is probably given in
[Ro]). But the general question is still widely open.
Computer algebra could be used to provide evidence for such conjectures (or, to
produce counter examples) provided one can solve the following
problems:
- find algorithms to compute the 0-dimensional ideals (related to the
above problems). In many cases this is easy but for others this is unknown
(e.g., to compute the equisingularity ideal for a sufficiently general
singularity);
- find fast algorithms to compute the intersection of
zero-dimensional ideals. The general method for computing intersections via
syzygies or elimination is too slow, due to the high complexity of the
algorithms involved. There is already some considerable progress made, by
the so-called Buchberger-Möller algorithm and further generalisations
(cf. [AKR]), but certainly this is not yet sufficient.


Next: Symbolic-numerical polynomial solving
Up: Applications of Computer Algebra
Previous: Moduli spaces and invariants
Christoph Lossen
2001-03-21
![]() of degree
of degree ![]() :
by the genus formula
:
by the genus formula ![]() can have, at most,
can have, at most,
![]() singularities. Another upper bound for the (weighted) number of singularities
arises from
applying Bézout's Theorem to the intersection of two generic polars of
singularities. Another upper bound for the (weighted) number of singularities
arises from
applying Bézout's Theorem to the intersection of two generic polars of ![]() :
:
![]() ,
we have the following existence theorem, which is asymptotically optimal (with
respect to the occurring invariants and the exponent of
,
we have the following existence theorem, which is asymptotically optimal (with
respect to the occurring invariants and the exponent of ![]() )
)
![]() .
.
![]() , e.g.,
, e.g.,
![]() ,
,
![]() in general position,
in general position, ![]() a positive integer, and let
a positive integer, and let
![]() . Then the
Hilbert function satisfies
. Then the
Hilbert function satisfies
![]() ,
,
![]() in
general position,
in
general position, ![]() positive integers, and let
positive integers, and let
![]() denote the minimal degree
of a curve passing through each of the points
denote the minimal degree
of a curve passing through each of the points ![]() with multiplicity
(at least)
with multiplicity
(at least) ![]() ,
, ![]() . Then
. Then