4. Suggestions for the algorithms

Here I would like to propose a variant of the algorithm for global (quasi-)homomogeneous ideals or modules realizing the ideas of the Sections 3.2 and 3.3. The main question is, whether the usage of Hilbert functions yields better restrictions to the pair sets than the regularity does. This will (hopefully) be answered in the near future by programming it in SINGULAR.

$S={\bf Res}(F)$
INPUT: $F=\{g_1,\ldots,g_n\}$ generators of the given ideal,
OUTPUT: $S=\{S_1,\ldots,S_n\}$ the resolution of F,

(F',Syz_F)=computeFirstSyzygies(F)

S'=resolve(In(F'))

hilb_.=computeHilbertFunctions(S')

L=buildPairs(Syz_F)

i=1

WHILE ( $L \not= \emptyset$)

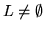h=0 //the Hilbert function of the actual module S_i

$L'=\emptyset$

deg=deg_min

WHILE ( isNotComplete(h,hilb_i))

G=reduce(L',deg,hilb_i,h)

L'=buildPairs(G)

h=computeHilbertFunction(G)

WHILE ( isNotComplete(h,hilb_i,deg))

$G=G\cup reduce(L,deg,hilb_i,h)$

h=computeHilbertFunction(G)

checkForDirectReductions(L,S_i-1,deg,hilb_i)

deletePairs(L,deg)

deg=deg+1

S_i=G

L=L'

i=i+1

The main content of the above procedures is

$$\begin{array}{ll} \mbox{computeFirstSyzygies} &\mbox{is the ... ...eletePairs} & \mbox{cancels superfluous pairs.}\\ \end{array}$$