2 Pointer TypeSpec and recursive data structures

 

It is important to be able to handle the idea of a ``pointer'', especially since this is how recursive data structures are done. This is accomplished with the MP_Pointer common operator appearing in a common meta operator packet.

<Pointer TypeSpec>  ::=  
    CommonMetaOperatorPkt(MP_Pointer) <Pointer AP> 
 
<Pointer AP> ::= 
    AP(MP_PrototypeAnnot) | AP(MP_RecursiveStructAnnot) 
    | AP(MP_RecursiveUnionAnnot)

The number of arguments to the operator within the Prototype tree must be 0. Consequently, the number of arguments to the pointer type must be given explicitly in the data packet as an IMP_Uint32 whose value is either 0, indicating a NULL pointer, or 1, indicating that the pointer ``points to" a block of data. This data immediately follows the ``1" in the data packet. For non-recursive objects, the structure of this data is given by a prototype to the MP_Pointer operator.

Recursive data objects are just a special case of structures or unions. The annotations MP_RecursiveStructAnnot (MP_RecursiveUnionAnnot) are attached to the struct (union) operator packet and to the CMOP(MP_Pointer) packet to indicate their recursive nature. A recursive pointer always points back to the most closely nested recursive structure or union within the prototype tree. This approach admittedly provides a limited ``namespace'', but it is our opinion that it will support the majority of needs, and, in keeping with the KISS principle, we chose not to go immediately to a true naming mechanism. However, using an annotation to indicate recursion is a general approach that can easily be extended simply by adding a naming annotation.

As before, MP_Pointer always has 0 in its number of arguments field. Consequently, the actual number of arguments must be read from the data packet which follows the prototype tree. This value must be 0 (NULL pointer) or 1 (non-NULL pointer). An accurate mental model of such a structure is a linked list.

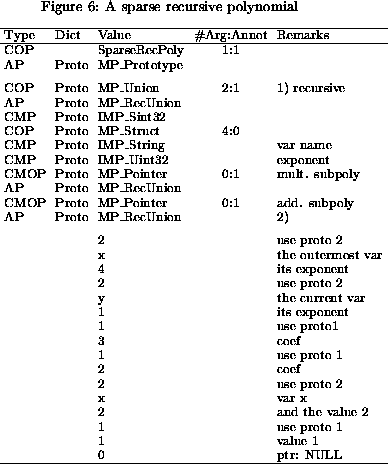
A last example uses MP_Union, MP_Struct, MP_Pointer, in MP_RecUnion to represent a sparse recursive polynomial (see Figure 6). Notice how naturally the definition below is described in the prototype between lines 1 and 2.

union SparseRecPoly  {
  Sint32;                        // coefficient
  struct exponent {
   String;                       // varname
   Uint32;                       // exponent
   Pointer struct SparseRecPoly; // multiplic subpoly
   Pointer struct SparseRecPoly; // additive subpoly
  };
};

The sample data is:
3*x^4(y+2) + x^2 = x^4 + x^2
*
(y + 2)
*
3

  

Figure 6: A sparse recursive polynomial