4. Relating the Word and Ideal Membership Problems in Groups and Free Group Rings

In this section we want to point out how the Gröbner basis methods as introduced in [MaRe93,Re95] for general monoid rings when applied to group rings are related to the word problem. First we state that similar to theorem 1 the word problem for groups is equivalent to a restricted version of the membership problem for ideals in a free group ring. Let the group be presented by a string rewriting system $(\Sigma, T \cup T_{I})$ such that there exists an involution $\imath: \Sigma \longrightarrow\Sigma$, i.e for all $a \in \Sigma$ we have $\imath(a) \neq a$, $\imath(\imath(a)) = a$, and the $T_{I}= \{(a\imath(a), \lambda) \mid a \in\Sigma \}$. Every group has such a presentation. Notice that the set of rules T_I is confluent with respect to any admissible ordering on $\Sigma$. By ${\cal F}_{\Sigma}$ we will denote the free group with presentation $(\Sigma, T_{I})$. The elements of ${\cal F}_{\Sigma}$ will be represented by freely reduced words, i.e. we assume that the words do not contain any subwords of the form $a\imath(a)$.

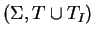
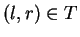
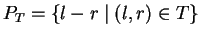
Theorem 6 ([Re95,MaRe95])   Let $(\Sigma, T \cup T_{I})$ be a finite string rewriting system presenting a group and without loss of generality for all $(l,r) \in T$ we assume that l and r are free reduced words. We associate the set of polynomials $P_T= \{ l-r \mid (l,r) \in T \}$ in ${\bf K}[{\cal F}_{\Sigma}]$ with T.
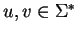
Then for $u,v \in \Sigma^*$ the following statements are equivalent:

(1)

$u \mbox{$\,\stackrel{*}{\longleftrightarrow}\!\!\mbox{}^{{\rm }}_{T \cup T_{I}}\,$ } v$.

(2)

$u\!\!\downarrow_{T_{I}} -v\!\!\downarrow_{T_{I}} \in {\sf ideal}_{}^{}(P_T)$.

Proof : 1.11.1 
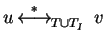$1 \Longrightarrow2:$
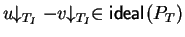
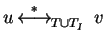
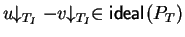