


Next: 4. Relating the Word
Up: Relating Rewriting Techniques on
Previous: 2. Presentations: Congruences in
3. Relating the Word and the
Ideal Membership Problems in Monoids and Free Monoid Rings
Let us start this section with some algebraic notions concerning monoid
rings.
For a monoid 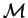 with multiplication
with multiplication 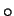 and a total well-founded
ordering
and a total well-founded
ordering 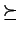 on
on 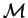 ,
the elements of the monoid ring
,
the elements of the monoid ring
![${\bf K}[{\cal M}]$](img80.gif) over a field
over a field 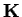 can
be presented as ``polynomials''
can
be presented as ``polynomials''
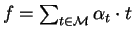 where only finitely many
where only finitely many
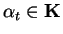 are non-zero.
The elements
are non-zero.
The elements
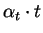 are called monomials consisting of a
coefficient
are called monomials consisting of a
coefficient 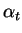 and a term t.
Addition and multiplication
for two polynomials
and a term t.
Addition and multiplication
for two polynomials
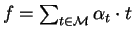 and
and
 is defined as
is defined as
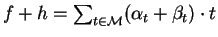 and
and
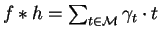 with
with
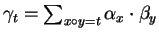 .
Given a non-zero polynomial p in
.
Given a non-zero polynomial p in
![${\bf K}[{\cal M}]$](img80.gif) ,
the head term
,
the head term
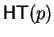 is the
largest term in p with respect to
is the
largest term in p with respect to 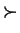 ,
which has non-zero coefficient
denoted by
,
which has non-zero coefficient
denoted by
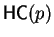 ,
and the head monomial is
,
and the head monomial is
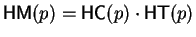 .
.
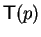 is the set of all
is the set of all
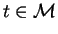 with non-zero coefficient in p.
For a subset F of
with non-zero coefficient in p.
For a subset F of
![${\bf K}[{\cal M}]$](img80.gif) we call the set
we call the set
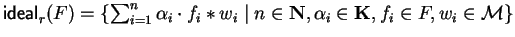 5 the right ideal,
5 the right ideal,
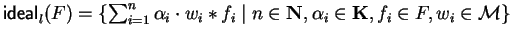 the left ideal and
the left ideal and
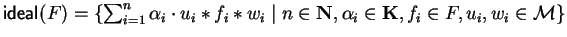 the two-sided ideal
generated by F.
By
the two-sided ideal
generated by F.
By
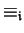 we will denote the (right, left respectively two-sided) congruence
induced by a (right, left respectively two-sided) ideal
we will denote the (right, left respectively two-sided) congruence
induced by a (right, left respectively two-sided) ideal
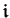 on
on
![${\bf K}[{\cal M}]$](img80.gif) .
.
The following theorem states that the word problem for monoids
is equivalent to a restricted version of the ideal membership
problem in free monoid rings.
This immediately implies the undecidability of the latter problem which is also
stated in [Mo87,KaWe90], but the proof we give here
provides a stronger result outlined below.
For a string rewriting system
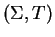 presenting a
monoid, the related free monoid ring is
presenting a
monoid, the related free monoid ring is
![${\bf K}[\Sigma^*]$](img102.gif) ,
where
,
where 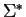 is the free monoid generated by
is the free monoid generated by 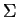 with word concatenation as binary operation and
with word concatenation as binary operation and 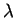 as identity element.
as identity element.
Theorem 1
Let
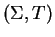
be a finite string rewriting system presenting a monoid
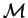
and
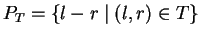
a set of polynomials in
![${\bf K}[\Sigma^*]$](img102.gif)
associated with
T.
Then for
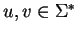
the following statements are equivalent:
- (1)
-
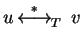 ,
i.e. the relation u=v holds in
,
i.e. the relation u=v holds in 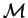 .
.
- (2)
-
 .
.
Proof :
1.11.1



Next: 4. Relating the Word
Up: Relating Rewriting Techniques on
Previous: 2. Presentations: Congruences in
| ZCA Home |
Reports |
![]() presenting a
monoid, the related free monoid ring is
presenting a
monoid, the related free monoid ring is
![]() ,
where
,
where ![]() is the free monoid generated by
is the free monoid generated by ![]() with word concatenation as binary operation and
with word concatenation as binary operation and ![]() as identity element.
as identity element.