


Next: 4. Splitting criteria
Up: Splitting algorithm for vector
Previous: 2. Block type Bruhat
(3.1)
In virtue of Lemma 2 we shall look for presentation matrices
which have a good chance of being equivalent to a matrix in block diagonal form.
Definition 3
For a given
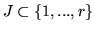
we call
Q a
J-row-minimal matrix if
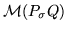
is minimal in the set of
Rk-submodules
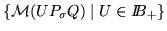
,
where
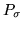
is a permutation matrix such that the associated permutation
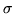
maps
J to
J0.
Obviously, this notation is independent of the choice of 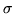 .
Moreover,
Q is called row-minimal if it is J-row-minimal with
respect to all strict subsets J of row indices
.
Moreover,
Q is called row-minimal if it is J-row-minimal with
respect to all strict subsets J of row indices
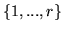 .
.
(3.2)
The test for whether a module M will split is based on
the observation that a presentation matrix of M in block diagonal form
Q0 is
J0- and J'0-row-minimal (cf. Lemma 2).
It is possible to check by a standard basis computation
whether a row-minimal matrix Q is equivalent
to a block diagonal matrix.
To do that, we have to fix an arbitrary (local) monomial order
of Rr, ordering first by components; that is,
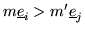 for any two monomials
for any two monomials 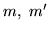 and
and
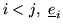 the i-th unit
column.
the i-th unit
column.
(3.3)
Let 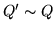 be a matrix formed by an ordered standard basis of
be a matrix formed by an ordered standard basis of
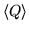 .
From the above order we obtain an integer l
such that all
columns of Q' having index l'> l will have their first
non-zero entry in the k'-th component, k'>k. Hence Q' will
have the block structure
.
From the above order we obtain an integer l
such that all
columns of Q' having index l'> l will have their first
non-zero entry in the k'-th component, k'>k. Hence Q' will
have the block structure
and the modules associated to A' and D' are characterized by Q:
Changing the roles of J0 and J'0 (resp. reversing the order
of components)
we may write a corresponding standard basis Q'' in analogous block form
Comparing these two different standard bases of Q, we obtain as a trivial
consequence
Lemma 4
With the notation from above
(3.4)
Usually we are not in this situation and we first have to apply row operations.
But, assuming J0-row-minimality, it is enough to apply only those
row-operations belonging to 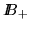 :
:
Proposition 5
If
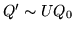
for some
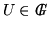
and
if
Q' is
J0-row-minimal, then
(i1)
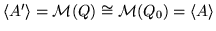
(i2)
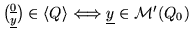 ;
that is,
;
that is,
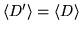 .
.
(i0)
First note that given an isomorphism
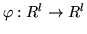 and a
and a
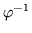 -invariant submodule
-invariant submodule
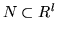 ,
then N is
,
then N is 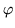 -invariant, too (otherwise
-invariant, too (otherwise
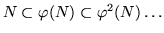 would produce an infinite
ascending chain!).
would produce an infinite
ascending chain!).
(i1) With the notation of (3.3) let
Letting
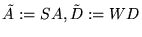 ,
,
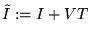 ,
we obtain
,
we obtain
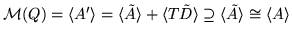 .
Because of the minimality assumption,
.
Because of the minimality assumption,
Again, by Lemma 1(i3),
we have a factorization
Consequently, we obtain
and, by the initial remark,
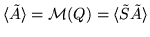 .
.
(i2) An easy computation shows that
Thus,
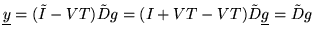 ,
which shows that
,
which shows that
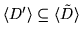 .
On the other hand
.
On the other hand
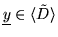 implies the existence of a
implies the existence of a
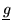 such that
such that
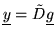 .
Because
.
Because
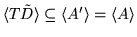 ,
there is an
,
there is an
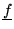 such that
such that
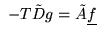 ;
that is,
;
that is,
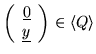 and
and
 .
.



Next: 4. Splitting criteria
Up: Splitting algorithm for vector
Previous: 2. Block type Bruhat
| ZCA Home |
Reports |
![]() for any two monomials
for any two monomials ![]() and
and
![]() the i-th unit
column.
the i-th unit
column.
![]() be a matrix formed by an ordered standard basis of
be a matrix formed by an ordered standard basis of
![]() .
From the above order we obtain an integer l
such that all
columns of Q' having index l'> l will have their first
non-zero entry in the k'-th component, k'>k. Hence Q' will
have the block structure
.
From the above order we obtain an integer l
such that all
columns of Q' having index l'> l will have their first
non-zero entry in the k'-th component, k'>k. Hence Q' will
have the block structure
![]() :
:
![]() .
.
 and
and