


Next: 5. Criteria for row-minimality
Up: Splitting algorithm for vector
Previous: 3. Row-minimal matrices
(4.1)
Next we want to characterize those row-minimal matrices belonging to a
decomposable module. The idea comes from the fact that the canonical homomorphism
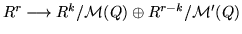 factors via M
and that the induced surjection
factors via M
and that the induced surjection
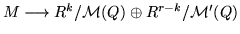 is an isomorphism. Hence, it reflects a direct sum decomposition
of M if and only if Q is equivalent to a block diagonal matrix Q0. Then Q is necessarily row-minimal with respect to J0 and J'0.
is an isomorphism. Hence, it reflects a direct sum decomposition
of M if and only if Q is equivalent to a block diagonal matrix Q0. Then Q is necessarily row-minimal with respect to J0 and J'0.
Proposition 6
If
Q is row-minimal, then
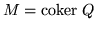
is decomposable if and only if for some
permutation
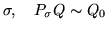
.
Assume M splits. Then we know
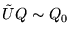 and,
for some permutation
and,
for some permutation 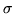 ,
,
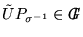 ;
i.e.,
;
i.e.,
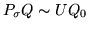 and
and
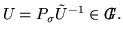 By Proposition 5(i2), we obtain
By Proposition 5(i2), we obtain
The same holds for J'0 , because Q is J'0-row-minimal, too; that is,
But then the composition of the canonical surjection
with
must be an isomorphism, showing
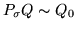 .
.
Note:
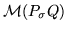 and
and
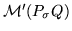 are computed by a standard
basis computation with respect to a certain module ordering in the components.
So we simply have to check whether
are computed by a standard
basis computation with respect to a certain module ordering in the components.
So we simply have to check whether
has a solution X, which corresponds to a simple syzygy computation.
(4.2)
Before computing a solution X, it is necessary for Q to be row-minimal,
which may be tested using methods discussed in the next section. Usually
Q is not row-minimal, in which case we shall use an algorithm to
transform Q into an equivalent and J0-row-minimal matrix.
But we do not know a procedure
to obtain row-minimality for all subsets immediately.
Hence we shall formulate a second version of
the splitting criteria.
Proposition 7
If
Q is
J0-row-minimal, then
By Proposition 5, it follows that
then
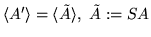 and
and
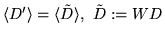 .
Therefore
.
Therefore
and
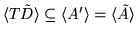 ,
giving
,
giving
from which it may be concluded that
The other direction is obvious.
Note:
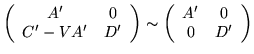 if and only if
C' - VA' = D'V'
for some V'; i.e. we obtain
if and only if
C' - VA' = D'V'
for some V'; i.e. we obtain
Corollary 8
If
Q is
J0-row-minimal,
then for an ordered standard basis
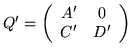
of
Q we have:
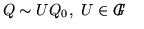
if and only if

the equation
VA'+
D'
V'=
C' has a solution (
V,
V').
Deciding the solvability of the above equation is reduced to
a lifting computation: Let 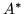 and
and 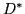 be matrices corresponding
to
be matrices corresponding
to
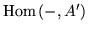 and
and
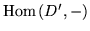 ,
and let [V], [V'], [C']
denote flattenings to a column vector of
V, V', C', respectively. Then we obtain
,
and let [V], [V'], [C']
denote flattenings to a column vector of
V, V', C', respectively. Then we obtain
that is, [C'] can be lifted to
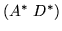 if and only if the
equation has a solution.
if and only if the
equation has a solution.



Next: 5. Criteria for row-minimality
Up: Splitting algorithm for vector
Previous: 3. Row-minimal matrices
| ZCA Home |
Reports |
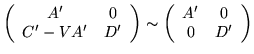 if and only if
C' - VA' = D'V'
for some V'; i.e. we obtain
if and only if
C' - VA' = D'V'
for some V'; i.e. we obtain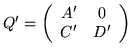 of Q we have:
of Q we have: