


Next: 3. Defining Reduction in
Up: String Rewriting and Gröbner
Previous: 1. Introduction
2. Fundamental Relations Between Semi-Thue Systems and Monoid Rings
Kandri-Rody and Weispfenning have shown in [KaWe90] that
the ideal membership problem for finitely
generated two-sided ideals is algorithmically unsolvable
for the free monoid ring
![${\bf Q}[\{ X_1, X_2 \}^*]$](img124.gif) by reducing the
halting problem for Turing machines to this problem.
Here we state a similar result by showing that the word problem for
semi-Thue systems is equivalent to a restricted version of the ideal membership
problem in free monoid rings
by reducing the
halting problem for Turing machines to this problem.
Here we state a similar result by showing that the word problem for
semi-Thue systems is equivalent to a restricted version of the ideal membership
problem in free monoid rings
![${\bf K}[\Sigma^*]$](img125.gif) where
where  is a finite alphabet.
is a finite alphabet.
Theorem 2..1
Let

be a finite semi-Thue system and
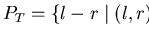
a set of polynomials associated with
T.
Then for
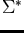
the following statements are equivalent:
- (1)
-
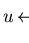 .
.
- (2)
-
![$u-v \in {\sf ideal}_{}^{{\bf K}[\Sigma^*]}(P_T)$](img129.gif) .
.
The existence of a finite semi-Thue system over an alphabet with
two elements having undecidable word problem yields that the ideal
membership problem for free monoid rings with more than one generator is
undecidable.
In case the free monoid is generated by one element, we have decidable
ideal membership problem.
In fact this is the ordinary polynomial
ring in one variable and, e.g., the Euclidean algorithm can
be applied to solve the ideal membership problem.
Perhaps less obvious is that
the word problem for finitely presented groups is similarly equivalent
to a restricted version of the membership problem for ideals in a
free group ring.
Let the group be presented by a semi-Thue system
 such that there exists an
involution
such that there exists an
involution
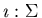 such that for all
such that for all
 we have
we have
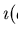 ,
,
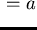 ,
and
the rules
,
and
the rules
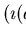 and
and
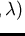 are
included in T.
Such systems are called group systems.
are
included in T.
Such systems are called group systems.
Theorem 2..2
Let
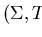
be a finite group system and
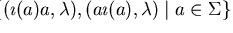
,
i.e.,
is a presentation of a free group

.
Further we can associate a system of polynomials
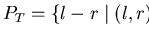
with
T and without loss of generality we can assume
that
l and
r are in normal form with respect to
TI.
Then for
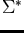
the following statements are equivalent:
- (1)
-
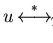 .
.
- (2)
-
![$u\!\!\downarrow_{T_{I}} -v\!\!\downarrow_{T_{I}} \in {\sf ideal}_{}^{{\bf K}[{\cal F}]}(P_T)$](img141.gif) .
.
As before, the existence of a finite group presentation over four
letters (resulting from two generators) with unsolvable word problem
implies that the ideal membership problem for free group rings with
more than one generator is undecidable.
Groups with one generator are known to have decidable word problem.
The ideal membership problem for free group rings with one generator is
solvable as this ring corresponds to the ring of Laurent polynomials
for the (commutative) free group with one generator.
Definition 2..3 (Mora)
Let

be a total admissible well-founded ordering on

used to sort the terms in the polynomials in decreasing order.
Further let
![$p = \sum_{i = 1}^{n} \alpha_{i} \cdot w_{i}, g = \sum_{j = 1}^{m} \beta_{j} \cdot v_{j}
\in {\bf K}[\Sigma^*]$](img143.gif)
.
We say
g reduces p to
q at a monomial
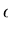
of
p in one step, denoted by
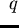
,
if
- (a)
-
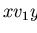 for some
for some
 ,
where
,
where
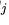 ,
,
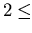 ,
and
,
and
- (b)
-
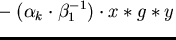 .
.
We write
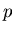
if there is a polynomial
q as defined above.
We can define

,

and reduction by a set
![$F \subseteq {\bf K}[\Sigma^*]$](img153.gif)
as usual.
Notice that for a set of polynomials F,
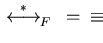 holds and
if additionally
holds and
if additionally
 is confluent we call F a Gröbner basis
of
is confluent we call F a Gröbner basis
of
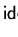 .
.
While theorem 2.1 reduces the word problem for semi-Thue systems
to the ideal membership problem in free monoid rings, reviewing the
proof of this theorem (compare page ![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/cross_ref_motif.gif) ) we see that
in fact the existence of finite convergent semi-Thue systems
corresponds to the existence of finite Gröbner bases and vice versa.
Hence solvable word problem does not imply the existence of finite Gröbner
bases as the example of a finitely presented monoid
) we see that
in fact the existence of finite convergent semi-Thue systems
corresponds to the existence of finite Gröbner bases and vice versa.
Hence solvable word problem does not imply the existence of finite Gröbner
bases as the example of a finitely presented monoid
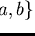 ,
,
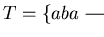 with solvable word problem but no finite
convergent presentation with respect to any admissible ordering
shows (see [KaNa85b]).
The ideal generated by the polynomial aba - bab in
with solvable word problem but no finite
convergent presentation with respect to any admissible ordering
shows (see [KaNa85b]).
The ideal generated by the polynomial aba - bab in
![${\bf K}[\{a,b\}^*]$](img159.gif) has no finite Gröbner basis with respect to any admissible ordering
on
has no finite Gröbner basis with respect to any admissible ordering
on  .
Notice that in this example we can apply a so called Tietze transformation
to the semi-Thue system, i.e. we can change the presentation without
changing the monoid, giving us the equivalent presentation
.
Notice that in this example we can apply a so called Tietze transformation
to the semi-Thue system, i.e. we can change the presentation without
changing the monoid, giving us the equivalent presentation
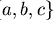 ,
,
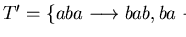 which can be successfully completed, e.g. with respect to the
length-lexicographical ordering with precedence
which can be successfully completed, e.g. with respect to the
length-lexicographical ordering with precedence
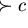 resulting in
resulting in
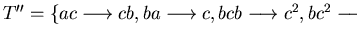 .
Similarly the ideal generated by
.
Similarly the ideal generated by
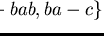 has a
finite Gröbner basis with respect to the same ordering.
Due to the result of Squire in [Sq87] there are finitely presented
monoids with solvable word problem which have no finite convergent
presentations and his examples give rise to finitely generated ideals in free
monoid rings with solvable ideal membership problem which have no
finite Gröbner bases.
has a
finite Gröbner basis with respect to the same ordering.
Due to the result of Squire in [Sq87] there are finitely presented
monoids with solvable word problem which have no finite convergent
presentations and his examples give rise to finitely generated ideals in free
monoid rings with solvable ideal membership problem which have no
finite Gröbner bases.
So now we have seen that since finitely generated ideals in
free monoid rings can
have unsolvable membership problem, in general they cannot
admit finite Gröbner bases.
It even is possible for a finitely generated ideal to admit a finite Gröbner basis with respect
to one admissible
ordering and none with respect to another admissible ordering.
On the other hand, in [Mo85] Mora provided a procedure which given an admissible
ordering enumerates a Gröbner basis with respect to this ordering.
This procedure terminates in case a finite Gröbner basis with
respect to the given ordering exists.
Hence the question might arise, whether it is possible to decide for a
finite set of polynomials and an admissible ordering
whether a finite Gröbner basis with respect to this
ordering exists.
This turns out to be
undecidable.
Theorem 2..4
It is undecidable, whether a finitely generated ideal
has a finite Gröbner basis in
the free monoid ring
![${\bf K}[\{ s,t \}^*]$](img166.gif)
with respect
to two-sided reduction as defined in
definition
2.3.
This result holds even assuming solvable membership problem for the ideal
[Sa96].
Corollary 2..5
It is undecidable, whether for a finitely generated ideal in
![${\bf K}[\{ s,t \}^*]$](img166.gif)
there exists a total, well-founded, admissible ordering on

such that
the ideal has a finite Gröbner basis with respect to reduction as defined
in
2.3.
Hence, for two-sided ideals the case of free monoids is already hard
although free monoids allow simple presentations by semi-Thue systems,
namely empty sets of defining relations.
In theorem 2.2 we have shown that the word
problem for group presentations is reducible to a restricted version of the
ideal membership problem for a free group ring.
We will show now that a similar result holds for the right ideal
membership problem in group rings.
Definition 2..6
Given a subset
S of a group

,
let

denote
the subgroup generated by
S.
The
generalized word problem or
subgroup problem is then to
determine, given

,
whether
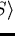
.
The word problem for a group  is just the generalized word problem
for the trivial subgroup in
is just the generalized word problem
for the trivial subgroup in  .
Thus the existence of a group with undecidable word problem yields
undecidability for the subgroup problem.
On the other hand, decidable word problem for a group does not
imply decidable generalized word problem.
.
Thus the existence of a group with undecidable word problem yields
undecidability for the subgroup problem.
On the other hand, decidable word problem for a group does not
imply decidable generalized word problem.
The next theorem states that the subgroup problem for a group is
equivalent to a special instance of the right ideal membership problem in
the corresponding group ring.
Theorem 2..7
Let
S be a finite subset of

and
![${\bf K}[{\cal G}]$](img172.gif)
the group ring
corresponding to

.
Further let
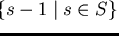
be a set of polynomials
9
associated to
S.
Then the following statements are equivalent:
- (1)
-
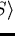 .
.
- (2)
-
 .
.
This theorem implies that when studying group rings we can only expect those over groups with solvable
generalized word problem to allow solvable membership problem for
right ideals.
Moreover, reviewing the proof (compare page ![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/cross_ref_motif.gif) )
we find that again reduction relations in semi-Thue systems
are related to right ideal congruences and vice versa.
In section 4 and 5 we
will see how this leads to strong connections to known solutions of
the subgroup problem by rewriting methods.
So appropriate candidates are e.g. free, Abelian, nilpotent and polycyclic groups.
On the other hand, solvable subgroup problem only implies the
solvability of a restricted version of the right ideal membership problem.
)
we find that again reduction relations in semi-Thue systems
are related to right ideal congruences and vice versa.
In section 4 and 5 we
will see how this leads to strong connections to known solutions of
the subgroup problem by rewriting methods.
So appropriate candidates are e.g. free, Abelian, nilpotent and polycyclic groups.
On the other hand, solvable subgroup problem only implies the
solvability of a restricted version of the right ideal membership problem.



Next: 3. Defining Reduction in
Up: String Rewriting and Gröbner
Previous: 1. Introduction
| ZCA Home |
Reports |
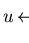 .
.
![$u-v \in {\sf ideal}_{}^{{\bf K}[\Sigma^*]}(P_T)$](img129.gif) .
.
![${\bf K}[\Sigma^*]$](img125.gif) where
where ![]() such that there exists an
involution
such that there exists an
involution
![]() such that for all
such that for all
 we have
we have
![]() ,
,
![]() ,
and
the rules
,
and
the rules
![]() and
and
![]() are
included in T.
Such systems are called group systems.
are
included in T.
Such systems are called group systems. and reduction by a set
and reduction by a set
 is confluent we call F a Gröbner basis
of
is confluent we call F a Gröbner basis
of
![]() ) we see that
in fact the existence of finite convergent semi-Thue systems
corresponds to the existence of finite Gröbner bases and vice versa.
Hence solvable word problem does not imply the existence of finite Gröbner
bases as the example of a finitely presented monoid
) we see that
in fact the existence of finite convergent semi-Thue systems
corresponds to the existence of finite Gröbner bases and vice versa.
Hence solvable word problem does not imply the existence of finite Gröbner
bases as the example of a finitely presented monoid
![]() ,
,
![]() with solvable word problem but no finite
convergent presentation with respect to any admissible ordering
shows (see [KaNa85b]).
The ideal generated by the polynomial aba - bab in
with solvable word problem but no finite
convergent presentation with respect to any admissible ordering
shows (see [KaNa85b]).
The ideal generated by the polynomial aba - bab in
![]() has no finite Gröbner basis with respect to any admissible ordering
on
has no finite Gröbner basis with respect to any admissible ordering
on ![]() .
Notice that in this example we can apply a so called Tietze transformation
to the semi-Thue system, i.e. we can change the presentation without
changing the monoid, giving us the equivalent presentation
.
Notice that in this example we can apply a so called Tietze transformation
to the semi-Thue system, i.e. we can change the presentation without
changing the monoid, giving us the equivalent presentation
![]() ,
,
![]() which can be successfully completed, e.g. with respect to the
length-lexicographical ordering with precedence
which can be successfully completed, e.g. with respect to the
length-lexicographical ordering with precedence
![]() resulting in
resulting in
![]() .
Similarly the ideal generated by
.
Similarly the ideal generated by
![]() has a
finite Gröbner basis with respect to the same ordering.
Due to the result of Squire in [Sq87] there are finitely presented
monoids with solvable word problem which have no finite convergent
presentations and his examples give rise to finitely generated ideals in free
monoid rings with solvable ideal membership problem which have no
finite Gröbner bases.
has a
finite Gröbner basis with respect to the same ordering.
Due to the result of Squire in [Sq87] there are finitely presented
monoids with solvable word problem which have no finite convergent
presentations and his examples give rise to finitely generated ideals in free
monoid rings with solvable ideal membership problem which have no
finite Gröbner bases.
 denote
the subgroup generated by S.
The generalized word problem or subgroup problem is then to
determine, given
denote
the subgroup generated by S.
The generalized word problem or subgroup problem is then to
determine, given
![${\bf K}[{\cal G}]$](img172.gif) the group ring
corresponding to
the group ring
corresponding to