



Next: 2. The space of
Up: An algorithm for constructing
Previous: Contents
This paper is a continuation of a joint paper with B. Martin [MS]
dealing with the problem of direct sum decompositions. The techniques
of that paper are used to decide wether two modules are isomorphic or
not. An positive answer to this question has many applications - for
example for the classification of maximal Cohen-Macaulay module over local
algebras as well as for the study of projective modules. Up to now computer
algebra is normally dealing with equality of ideals or modules which depends on
chosen embeddings. The present algorithm allows to switch to isomorphism
classes which is more natural in the sense of commutative algebra and
algebraic geometry.
Let R be a finitely generated (local) k-algebra without zerodivisors. Let
M and M' be two modules given via minimal representation matrices
A and A'. Then
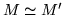 if and only if there are matrices
if and only if there are matrices
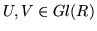 such that UAV=A'. We shall descibe a finite algorithm
to either compute the matrices U and V or to disprove isomorphism.
such that UAV=A'. We shall descibe a finite algorithm
to either compute the matrices U and V or to disprove isomorphism.




Next: 2. The space of
Up: An algorithm for constructing
Previous: Contents
| ZCA Home |
Reports |
![]() if and only if there are matrices
if and only if there are matrices
![]() such that UAV=A'. We shall descibe a finite algorithm
to either compute the matrices U and V or to disprove isomorphism.
such that UAV=A'. We shall descibe a finite algorithm
to either compute the matrices U and V or to disprove isomorphism.