



Next: 3. Finding a regular
Up: An algorithm for constructing
Previous: 1. Introduction
Throughout this paper we assume R to be a finitely generated, local
(or graded) k-algebra without zerodivisors and any (any graded) module
M as given as cokernel of a map of free modules. The presentation
matrix of this map is assumed to represent a minimal system of generators
of its image and is denoted by A(M) or simply A.
The case of a graded module is handled analogously. Therefore, we restrict
ourself to the local settings.
Let two modules M and M' be given by their representation matrices
A and A'. Assume the modules to be isomorphic. There are two
quadratic matrices U and V such that UAV=A'. By the above
properties of the representations both matrices have to be invertible,
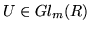 and
and
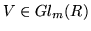 .
.
Now, let's look from the other side: Starting with two representation
matrices A and A' a necessary condition for an isomorphism of
the represented modules M and M' is an identical size of both
matrices. Denote this size by
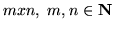 .
The sufficient
condition for an isomorphism is again the existence of matrices
.
The sufficient
condition for an isomorphism is again the existence of matrices
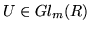 and
and
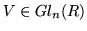 with UAV=A'. That means, we have to
resolve the equation
with UAV=A'. That means, we have to
resolve the equation
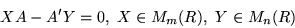 |
(1) |
and to look for a pair (X0,Y0) of regular matrices among all
solutions of (1).
First, we determine the module of all possible transformations
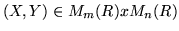 .
Let us consider the matrix A as map
.
Let us consider the matrix A as map
just by multiplying with A from the right. Analogously, we set
to be the map induced by the multiplication with A' from the left.
The map
given by
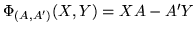 is a well defined module homomorphism
and its kernel is the module
Tr(A,A') of possible transformations.
Tr(A,A') can be computed in a single syzygy computation.
is a well defined module homomorphism
and its kernel is the module
Tr(A,A') of possible transformations.
Tr(A,A') can be computed in a single syzygy computation.




Next: 3. Finding a regular
Up: An algorithm for constructing
Previous: 1. Introduction
| ZCA Home |
Reports |
![]() and
and
![]() .
.
![]() .
The sufficient
condition for an isomorphism is again the existence of matrices
.
The sufficient
condition for an isomorphism is again the existence of matrices
![]() and
and
![]() with UAV=A'. That means, we have to
resolve the equation
with UAV=A'. That means, we have to
resolve the equation
![]() .
Let us consider the matrix A as map
.
Let us consider the matrix A as map