1 monomial operations

The basic monomial operations within GB computations are:

1.

Computations of the degree (resp. weighted degree):
the degree (resp. weighted degree) of a monomial $\alpha$ is the sum of the exponents $deg(\alpha):=\sum_{i=1}^n \alpha_i$ (resp. the weighted sum with respect to a weight vector w: $deg(\alpha):=\sum_{i=1}^n \alpha_i\,w_i$).

2.

Test for divisibility:
$\alpha \vert \beta \Leftrightarrow \forall i \in \{1..n\}: \alpha_i \le \beta_i$.

3.

Addition of two monomials:
$\gamma := \alpha + \beta \mbox{ with }\forall i \in \{1..n\}: \gamma_i=\alpha_i + \beta_i$.

4.

Comparison of two monomials with respect to a monomial ordering.

A monomial ordering > (term ordering) on the set of monomials M_n is a total ordering on M_n which is compatible with the natural semigroup structure, i.e., $\alpha > \beta$ implies $\gamma + \alpha > \gamma + \beta$ for any $\gamma \in M_n$. A monomial ordering is a well-ordering if $(0, \ldots, 0)$ is the smallest monomial. We furthermore call an ordering negative if $(0, \ldots, 0)$ is the largest monomial.

Robbiano (cf.[15]) proved that any monomial ordering > can be defined by a matrix $A \in GL(n, \bf {R})$: $\alpha > \beta \; \Leftrightarrow A \alpha >_{lex} A \beta$. Matrix-based descriptions of monomial orderings are very general, but have the disadvantage that their realization in an actual implementation is usually rather time-consuming. Therefore, they are not very widely used in practice.

Instead, the most frequently used descriptions of orderings have at most two defining conditions: a (possibly weighted) degree and a (normal or reverse) lexicographical comparison. We call such orderings simple orderings. The most important simple orderings (and their SINGULAR abbreviations) are:

• lexicographical (lp): used to eliminate variables and solve equations,
• (weighted) degree reverse lexicographical (dp): in general the most efficient one to compute a GB (as shown in [3]),
• (weighted) degree lexicographical (Dp),
• negative lexicographical ordering (ls),
• (weighted) negative degree reverse lexicographical (ds): also called tangent cone ordering,
• (weighted) negative degree lexicographical (Ds).

For monomials $\alpha, \beta \in M_n$ let

$$\begin{eqnarray*}\mbox{Lex}(\alpha, \beta) \!\!&\!\!=\!\!&\!\! \left\{\!\! \begi... ...pha) = \deg(\beta) \\ -1, \mbox{otherwise.} \end{array}\right. \end{eqnarray*}$$

Then we can define $\alpha > \beta$ for the above mentioned simple monomial orderings by:

$$\begin{array}{rlll} \mbox{lp:} \!\!\!&\!\!\! \!&\!\!\! \!\!&\... ...!\!\!&\!\! \mbox{RevLex}(\alpha, \beta) \!=\! 1 \\ \end{array}$$

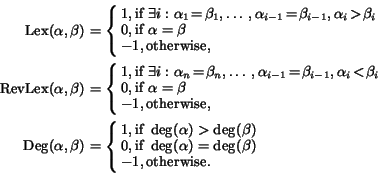
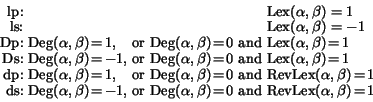
We furthermore call a monomial ordering > a degree based monomial ordering if $\forall \; \alpha, \beta: \deg(\alpha) > \deg(\beta) \Rightarrow \alpha > \beta$ (e.g., Dp and dp and their weighted relatives are degree based orderings).

Due to the nature of the GB algorithm, monomial operations are by far the most frequently used primitive operations. For example, monomial comparisons are performed much more often than, and monomial additions at least as often as, arithmetic operations over the coefficient field. The number of divisibility tests depends very much on the given input ideal, but is usually very large, as well (see also Table 1).

Nevertheless, whether or not monomial operations dominate the running time of a GB computation depends on the coefficient field of the underlying polynomial ring: monomial operations are certainly run-time dominating for finite fields with a small characteristic (e.g., integers modulo a small prime number), since an arithmetic operation over these fields can usually be realized much faster than a monomial operation. However, for fields of characteristic 0 (like the rational numbers), GB computations are usually dominated by the arithmetic operations over these fields, since the time needed for these operations is proportional to the size of the coefficients which tend to grow rapidly during a GB computation.

Therefore, improvements in the efficiency of monomial operations will have less of an impact on GB computations over fields of characteristic 0.