The PoSSo library [14] already uses parts of this idea to speed up monomial additions, assignments, and tests for equalities, but has not (yet?) carried these ideas over to the much more time-critical monomial comparisons and divisibility tests.
The details of this technique are based on the following lemma whose proof is straightforward and, therefore, omitted:
Lemma 1: Let
![]() ,
and
,
and
![]() with
with
![]() .
Furthermore, let
.
Furthermore, let
![]() and
and
![]() with
with
![]() such that
such that
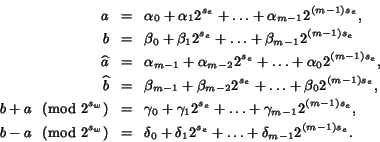
Lemma 1 shows how the monomial operations on the right-hand sides of (1) - (4) can be ``vectorized'', such that, on a 2's complement machine with word-size sw, the checks (resp. operations) on the left hand sides of (1) - (4) can be performed in at most three single machine instructions (see the source code examples below for further details).
However, before Lemma 1 can be applied in an actual implementation, some technical difficulties have to be overcome:
Firstly, stricter bounds on the values of the single exponents have to be assured (i.e., the exponent values need to be less than 2se -1 instead of 2se).
Secondly, the condition
![]() implies that the total length
of the exponent vector has to be a multiple of the word-size which
requires that
implies that the total length
of the exponent vector has to be a multiple of the word-size which
requires that
![]() ``unnecessary'' exponents (whose value is
set to and always kept at 0) might have to be added to the exponent
vector .
``unnecessary'' exponents (whose value is
set to and always kept at 0) might have to be added to the exponent
vector .
Thirdly, and most importantly, the order and arrangement of the exponents within the exponent vector has to be adjusted, depending on the monomial ordering and on the endianess of the used machine. On big-endian machines, the order of the exponents has to be reversed for reverse lexicographical orderings whereas on little-endian machines, the order of the exponents has to be reversed for lexicographical orderings. In practice, this fact can be hidden behind appropriate macro (or inline) definitions for accessing single exponents. In our implementation, we used a global variable called pVarOffSet and implemented the exponent access macro as follows:
#define pGetExp(p, i) \
p->exp[(pVarOffSet ? pVarOffSet - i : i)]
Provided that n is the number of variables of the current ring then we set the value of pVarOffSet as follows:
| type of machine | ||
| type of ordering | big-endian | little-endian |
| lexicographical | 0 | n-1 |
| reverse lexicographical | n-1 | 0 |
Some source code fragments can probably explain it best: Figure 1 shows (somewhat simplified) versions of our implementation of the vectorized monomial operations. Some explanatory remarks are in order:
n_w is a global variable denoting the length of the exponent
vectors in machine words (i.e., if sw is the size of a machine
word, se the size of an exponent, n the number of
variables, then
![]() ).
).
pLexSgn and pOrdSgn (used in MonComp) are global
variables which are used to appropriately manipulate the return value
of the comparison routine and whose values are set as follows:
| lp | ls | Dp | Ds | dp | ds | |
| pOrdSgn | 1 | -1 | 1 | -1 | 1 | -1 |
| pLexSgn | 1 | -1 | 1 | 1 | -1 | -1 |
Notice that MonAdd works on three monomials and it is most often used as a ``hidden'' initializer (or, assignment), since monomial additions are the ``natural source'' of most new monomials.
Our actual implementation contains various, tediously to describe, but more or less obvious, optimizations (like loop unrolling, use of pointer arithmetic, replacement of multiplications by bit operations, etc). We apply, furthermore, the idea of ``vectorized operations'' to monomial assignments and equality tests, too. However, we shall not describe here the details of these routines, since their implementation is more or less obvious and they have less of an impact on the running time than the basic monomial operations.
So much for the theory, now let us look at some actual timings: Table 1 shows various timings illustrating the effects of the vectorized monomial operations described in this section. In the first column, we list the used examples -- details about those can be found in the Appendix. All GB computations were done using the degree reverse lexicographical ordering (dp) over the coefficient field Z/32003. We measured the following times (all in seconds):
short
(for tn,s) and char (for tn,c)short
(for ts) and char (for tc).
Now, what do these numbers tell us?
Firstly, they support our assertion that for GB computations over finite fields of small characteristic, the running time is largely dominated by basic monomial operations (see column %mon). However, in which of the (three) basic monomial operations the most time is spent varies very much from example to example (compare, e.g., line ``gonnet'' with line ``ecyclic 6'').
Secondly, and most importantly: the impact of the vectorized monomial operations is quite substantial (see columns tn,s/ts, tn,c/tc which show the speedup gained by vectorized operations). As expected, the larger the ratio m = sw/se (i.e, the number of exponents packed in one machine word), the more speedup is usually gained (compare column tn,s/ts and tn,c/tc). However, notice that we cannot conclude a direct correlation between the percentage of time spent in monomial operations and the efficiency gains of vectorized operations. This is due to the fact that the number of inner loop iterations (and, hence, reduction of inner loop iterations) for comparisons and divisibility tests is not constant, but depends on the input monomials.
Thirdly: As we would expect, the more exponents are encoded into one
machine word, the faster the GB computation is accomplished (see the
ts/tc column). This has two main reasons: first, more
exponents are handled by one machine operation; and second, less
memory is used, and therefore, the memory performance increased (e.g.,
number of cache misses is reduced). However, we also need to keep in
mind that the more exponent are encoded into one word, the smaller are
the upper bounds on the value of a single exponents. This is
especially crucial for computations with char exponents, since
these require that an exponent may not be larger than 127. Ideally, we
would like to ``dynamically'' switch from one exponent size to the
next larger one, whenever it becomes necessary. With SINGULAR, we
cannot do this yet, at the moment, but we intend to implement this
feature in one of the next major upgrades.
Fourthly: We would like to point out that the only difference between
the SINGULAR versions resulting in t1.0 and tn,s is that
monomial comparisons for the different orderings are not reduced to
one inlined routine but instead are realized by function pointers (and,
therefore, each monomial comparisons requires a function call). Hence,
column
t1.0/tn,s shows that already the in-place realization of
monomial comparisons results in a considerable efficiency gain
which by far compensates the additional overhead incurred by the
additional indirection for accessing one (single) exponent value
(i.e., the overhead incurred by the pGetExp macro shown above).
Last, but not least, the combination of all these factors into our newest and fastest version of SINGULAR, leads to a rather significant improvement (see column t1.0/tc) over the ``old'' SINGULAR version 1.0.