- ... Reinert1
- The author was supported by the Deutsche Forschungsgemeinschaft (DFG).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... convergent2
- Convergent
presentations for groups are string rewriting systems which are terminating and confluent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ideals3
- An ideal is called
binomial if it has a basis solely consisting of polynomials of the form m1 -m2 where m1,m2 are monomials.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
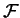 4
4
- Notice that while
 is minimal with respect to
is minimal with respect to  ,
the ordering is not compatible with multiplication as
,
the ordering is not compatible with multiplication as
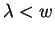 then would imply
then would imply
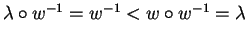 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...v5
- Those familiar with string rewriting systems should
notice that prefix reducing a word u with a binomial
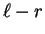 where
where  directly corresponds to prefix string reducing u with a rule
directly corresponds to prefix string reducing u with a rule 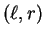 followed by free reduction.
followed by free reduction.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... algorithm6
- The FGLM Algorithm has been generalized to the
setting of finitely presented groups in [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reduction7
- We say a free reduced word
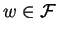 prefix reduces to v (modulo free
group reduction) using a rule
prefix reduces to v (modulo free
group reduction) using a rule
 if there exists
if there exists
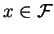 such that
such that
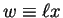 and
and
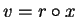 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... rule8
- Notice that there are trivial rules among these where the left and right hand sides coincide as
words and these of course have to be removed in order to make the system terminating.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... computed9
- The steps in the
computation of the prefix Gröbner basis can be directly related to Nielsen transformations (see [23]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... basis10
- The computation of the prefix Gröbner
basis is related to the filling of the first line of the tables in TC and the deduction of equations
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
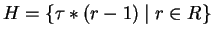 11
11
- The set H
realizes the addition of subgroup generators
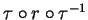 or in TC
corresponds to marking the first and last slot of each relator table with the newly found coset representative
or in TC
corresponds to marking the first and last slot of each relator table with the newly found coset representative
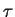 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... subgroup12
- This corresponds
to the coset collapses in TC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.