


Next: 5. Conclusions
Up: A Note on Nielsen
Previous: 3. Towards Gröbner Bases
4. Enumerating Cosets Using Gröbner Techniques
Let  ,
,
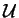 ,
,
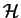 and
and  ,
R, U be as defined before.
In this section we combine the ideas presented in Section
3 in order to give a procedure with
the following output:
,
R, U be as defined before.
In this section we combine the ideas presented in Section
3 in order to give a procedure with
the following output:
- 1.
- If
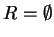 the procedure terminates with the monic prefix Gröbner basis G which allows to
decide the subgroup problem for the subgroup generated by U in
the procedure terminates with the monic prefix Gröbner basis G which allows to
decide the subgroup problem for the subgroup generated by U in
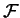 and to compute the Schreier coset
representatives (with respect to >).
The set
and to compute the Schreier coset
representatives (with respect to >).
The set
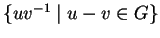 is Nielsen reduced for U.
is Nielsen reduced for U.
- 2.
- If
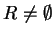 then, similar to
the Todd-Coxeter procedure, the procedure enumerates cosets of the subgroup generated by
then, similar to
the Todd-Coxeter procedure, the procedure enumerates cosets of the subgroup generated by
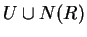 in
in
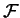 and on termination provides the set of all coset representatives of
and on termination provides the set of all coset representatives of
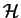 in
in
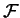 and
the multiplication table for the cosets with elements in
and
the multiplication table for the cosets with elements in
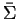 encoded in the prefix Gröbner basis.
encoded in the prefix Gröbner basis.
In contrast to TC we do not need the assumption that each generator occurs in at least one relator.
Let us start by giving an informal description of our procedure:
The input are encodings of the relators R and the subgroup generators U in
binomial sets
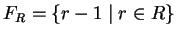 and
and
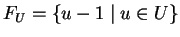 ,
respectively.
All ring operations take place in
,
respectively.
All ring operations take place in
![$\mathbb{K} [{\mathcal{F}}]$](img22.gif) .
The following sets are used by the procedure:
.
The following sets are used by the procedure:
- 1.
-
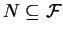 contains potential coset representatives of
contains potential coset representatives of
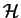 in
in
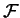 .
This set corresponds to the natural basis in
MATPHI.
.
This set corresponds to the natural basis in
MATPHI.
- 2.
-
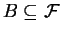 is a test set for possible coset representatives of
is a test set for possible coset representatives of
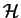 in
in
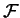 .
It corresponds to the border set in
MATPHI.
.
It corresponds to the border set in
MATPHI.
- 3.
-
![$H \subseteq \mathbb{K} [{\mathcal{F}}]$](img173.gif) is used to increment the generating set of the subgroup in order to achieve
a generating set for
is used to increment the generating set of the subgroup in order to achieve
a generating set for
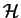 .
.
- 4.
-
![$G \subseteq \mathbb{K} [{\mathcal{F}}]$](img174.gif) is the monic prefix Gröbner basis which is used to decide, whether the candidates
in B are indeed coset representatives of the subgroup generated so far or not.
is the monic prefix Gröbner basis which is used to decide, whether the candidates
in B are indeed coset representatives of the subgroup generated so far or not.
In the first step, the procedure checks, whether the set of relators is empty.
If this is the case, the prefix Gröbner basis of the set FU is computed9
and the output
of the procedure is this basis, which allows to solve the subgroup problem for
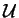 and can be transformed
into a Nielsen reduced set for U according to Theorem 7.
If the set of relators is not empty the procedure starts to enumerate cosets:
The set N is initialized with the empty word which is the coset representative of the
subgroup itself.
N will remain prefix closed throughout the computation, i.e. it will contain all prefixes of its elements.
The border set is
and can be transformed
into a Nielsen reduced set for U according to Theorem 7.
If the set of relators is not empty the procedure starts to enumerate cosets:
The set N is initialized with the empty word which is the coset representative of the
subgroup itself.
N will remain prefix closed throughout the computation, i.e. it will contain all prefixes of its elements.
The border set is
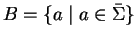 .
The set G contains the monic prefix Gröbner basis10
which allows to solve the subgroup problem for the
subgroup generated by
.
The set G contains the monic prefix Gröbner basis10
which allows to solve the subgroup problem for the
subgroup generated by 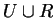 .
Now, while there are elements in B we proceed as follows:
The smallest element
.
Now, while there are elements in B we proceed as follows:
The smallest element 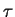 of B is removed.
Then if
of B is removed.
Then if 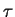 is not prefix reducible by G, it is added to N
and all border elements
is not prefix reducible by G, it is added to N
and all border elements 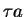 are added to B where
are added to B where
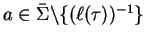 and
and
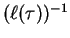 is the inverse of the last letter of the freely reduced word
is the inverse of the last letter of the freely reduced word 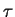 .
Moreover, we compute the auxiliary set
.
Moreover, we compute the auxiliary set
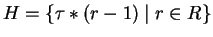 11.
In computing the monic prefix Gröbner basis of the set
11.
In computing the monic prefix Gröbner basis of the set 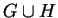 we are then able to solve the subgroup problem
for the subgroup now generated by the previous generating set extended by the generators
we are then able to solve the subgroup problem
for the subgroup now generated by the previous generating set extended by the generators
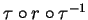 .
This of course corresponds to incrementally approaching the (infinite) generating set
.
This of course corresponds to incrementally approaching the (infinite) generating set
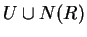 .
According to the new prefix Gröbner basis we have to ``correct'' our set of possible cosets N.
This is done by removing all elements with a prefix reducible with the new prefix Gröbner basis, as
these elements are no longer coset representatives of the incremented subgroup12.
Notice that this operation does not change the property of N of being prefix closed.
The procedure terminates as soon as the set B becomes empty.
.
According to the new prefix Gröbner basis we have to ``correct'' our set of possible cosets N.
This is done by removing all elements with a prefix reducible with the new prefix Gröbner basis, as
these elements are no longer coset representatives of the incremented subgroup12.
Notice that this operation does not change the property of N of being prefix closed.
The procedure terminates as soon as the set B becomes empty.
Procedure: EXTENDED TC SIMULATION
llGiven:
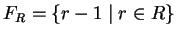 , a set of binomials encoding the relators.
, a set of binomials encoding the relators.
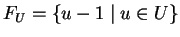 , a set of binomials encoding the subgroup generators.
[1ex]
, a set of binomials encoding the subgroup generators.
[1ex]
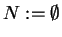 ;
if
;
if
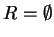 then
then
 ;
else
;
else
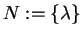 ;
;
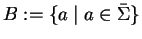 ;
;
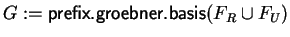 ;
while
;
while
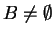 do
do
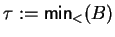 ;
;
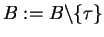 ;
if
;
if 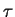 is not prefix reducible by G
then
is not prefix reducible by G
then
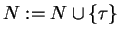 ;
;
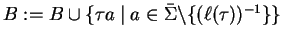 ;
;
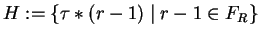 ;
;
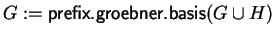 ;
;
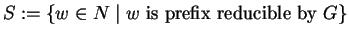 ;
;
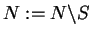 ;
endif
endwhile
endif
;
endif
endwhile
endif
On termination by construction N is either empty or a set of prefix closed coset representatives
with respect to the ordering >.
The latter is ensured as for each 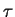 added to N the set B contains all border elements
added to N the set B contains all border elements
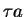 ,
,
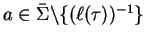 and removing the set of elements
and removing the set of elements
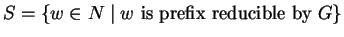 from
N does not destroy the property of being prefix closed.
from
N does not destroy the property of being prefix closed.
Moreover, we have the following important invariant for the case that R is not empty:
Let No, Bo, Go denote the sets when starting the execution of the while loop and
Nn, Bn, Gn the ones at the end.
Then for the sets Nn, Bn, and Gn at the end of each loop
we have that for each w which is not prefix reducible by Gn one of the following three conditions holds:
- 1.
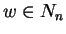 ,
or
,
or
- 2.
-
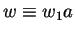 ,
,
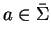 and
and
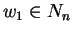 ,
,
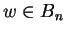 ,
or
,
or
- 3.
-
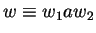 ,
,
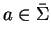 ,
,
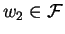 and
and
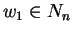 ,
,
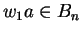 .
.
This is true for the sets
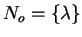 and
and
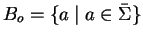 before
entering the while loop.
Notice that due to the construction the elements prefix irreducible with respect to Gn are
a (not necessarily proper) subset of those prefix irreducible with respect to Go.
In the loop first the smallest element
before
entering the while loop.
Notice that due to the construction the elements prefix irreducible with respect to Gn are
a (not necessarily proper) subset of those prefix irreducible with respect to Go.
In the loop first the smallest element 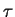 is removed from Bo.
If it is prefix reducible by Go the new sets are Nn = No,
is removed from Bo.
If it is prefix reducible by Go the new sets are Nn = No,
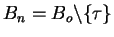 and Gn = Go and the property still holds, since then
and Gn = Go and the property still holds, since then 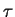 cannot be a prefix of any element
not prefix reducible by Gn.
Now if
cannot be a prefix of any element
not prefix reducible by Gn.
Now if 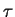 is not prefix reducible by Go it is first added to N and its border elements are
added to B.
We get
is not prefix reducible by Go it is first added to N and its border elements are
added to B.
We get
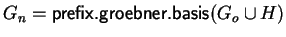 ,
,
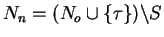 and
and
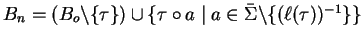 .
Let w be prefix irreducible with respect to Gn.
Then w was also prefix irreducible with respect to Go and we have to check the three possible cases:
.
Let w be prefix irreducible with respect to Gn.
Then w was also prefix irreducible with respect to Go and we have to check the three possible cases:
- 1.
- If
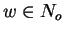 ,
since w is still prefix irreducible by Gn
it cannot be in S, hence
,
since w is still prefix irreducible by Gn
it cannot be in S, hence 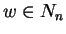 .
.
- 2.
- If
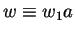 ,
,
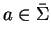 and
and
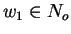 ,
,
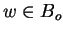 ,
as
,
as
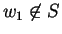 we find
we find
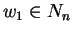 and either
and either
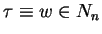 or
or 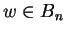 .
.
- 3.
- If
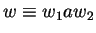 ,
,
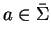 ,
,
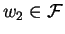 and
and
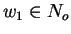 ,
,
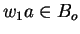 ,
again
as
,
again
as
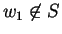 we find
we find
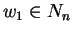 and
and
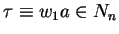 or
or
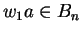 .
.
For non-empty R the procedure will only terminate when B becomes empty.
Then because of the invariant
the set N must contain all elements of
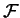 which are not prefix reducible by the final set G.
The next theorem now states that on termination the subgroup
which are not prefix reducible by the final set G.
The next theorem now states that on termination the subgroup
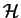 generated by
generated by
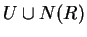 in
in
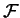 is in fact finitely generated (by
is in fact finitely generated (by
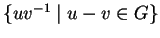 ).
G can be used to decide the subgroup problem for
).
G can be used to decide the subgroup problem for
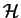 by prefix reduction.
Moreover, if R is not empty,
G contains the respective (non-trivial) equations which are also generated by TC and
encode the multiplication table for the cosets with generators as follows: For each polynomial xa - y
where
by prefix reduction.
Moreover, if R is not empty,
G contains the respective (non-trivial) equations which are also generated by TC and
encode the multiplication table for the cosets with generators as follows: For each polynomial xa - y
where
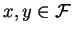 ,
,
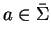 we know that x and y are coset representatives
and the corresponding entry in the table for x and a is
we know that x and y are coset representatives
and the corresponding entry in the table for x and a is
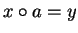 .
.
Theorem 9
Let
R and
U be as specified above.
If procedure E
XTENDED T
C S
IMULATION terminates, then the subgroup
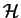
generated by
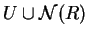
is finitely generated.
Proof:
If the set of relators is empty
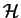 is generated by U and we are done.
On the other hand, for non-empty R
on termination the set G contains a prefix Gröbner basis which
can be used to decide the subgroup membership problem for the subgroup
is generated by U and we are done.
On the other hand, for non-empty R
on termination the set G contains a prefix Gröbner basis which
can be used to decide the subgroup membership problem for the subgroup
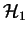 generated
by the set
generated
by the set
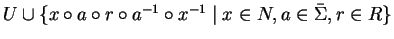 in
in
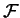 (compare Theorem 6).
We have to show that
(compare Theorem 6).
We have to show that
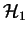 is in fact
is in fact
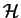 ,
the subgroup generated by
,
the subgroup generated by
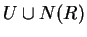 in
in
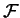 .
This is done by proving that for any
.
This is done by proving that for any
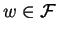 ,
,
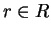 the element
the element
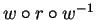 is in
is in
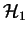 .
Let us assume
.
Let us assume
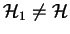 .
Then there is
.
Then there is
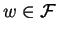 minimal with respect to > such that for appropriate
minimal with respect to > such that for appropriate 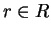 we have
we have
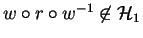 .
The case
.
The case 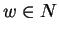 immediately gives us a contradiction to our construction.
Therefore, by our invariant w cannot be irreducible by G as this would imply
immediately gives us a contradiction to our construction.
Therefore, by our invariant w cannot be irreducible by G as this would imply 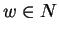 .
Hence let
.
Hence let
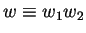 such that w1 is the head term of some polynomial w1 - v in G.
Then we know
such that w1 is the head term of some polynomial w1 - v in G.
Then we know
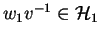 and
and
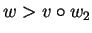 .
Now we get
.
Now we get
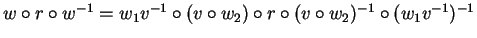 and as w was a minimal counter example
and as w was a minimal counter example
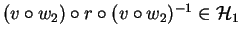 .
But this implies
.
But this implies
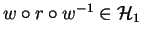 as
as
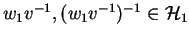 contradicting our assumption.
q.e.d.
contradicting our assumption.
q.e.d.
1.11
Now, if
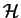 is finitely generated and contains a non-trivial normal subgroup then
is finitely generated and contains a non-trivial normal subgroup then
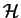 has finite index in
has finite index in
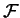 (Proposition 3.11 in [14]).
Since TC terminates in case
(Proposition 3.11 in [14]).
Since TC terminates in case
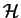 has finite index in
has finite index in
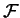 it remains to show that this is also the
case for procedure EXTENDED TC SIMULATION.
it remains to show that this is also the
case for procedure EXTENDED TC SIMULATION.
Theorem 10
Let
R and
U be as specified above.
If the subgroup generated by
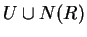
has finite index in
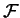
,
then procedure E
XTENDED T
C S
IMULATION terminates.
Proof:
Let the subgroup
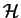 generated by
generated by
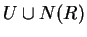 in
in
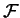 have finite index.
If the set of relators is empty then there is nothing to show.
The set of coset representatives can for example be computed by enumerating the set of elements
which are not prefix reducible by the obtained prefix Gröbner basis G of the right ideal generated
by FU.
have finite index.
If the set of relators is empty then there is nothing to show.
The set of coset representatives can for example be computed by enumerating the set of elements
which are not prefix reducible by the obtained prefix Gröbner basis G of the right ideal generated
by FU.
Hence let us assume that R is not empty.
As
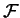 is finitely generated
is finitely generated
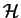 is also finitely generated (Proposition 3.9 in [14])
and hence has a finite Schreier transversal S.
Then for
is also finitely generated (Proposition 3.9 in [14])
and hence has a finite Schreier transversal S.
Then for 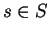 ,
,
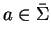 and every
and every 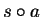 there exists just one
there exists just one 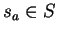 such that
such that
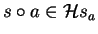 .
Since
.
Since
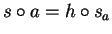 for some
for some
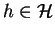 we have
we have
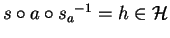 .
The set
.
The set
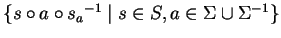 generates
generates
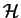 (compare Chapter 1 in [10]).
But then
(compare Chapter 1 in [10]).
But then
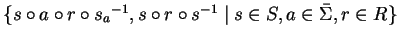 again
is a generating set for
again
is a generating set for
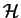 as
as
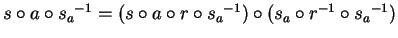 .
Hence the procedure will terminate at least after checking the candidates
.
Hence the procedure will terminate at least after checking the candidates 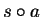 for
for 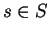 .
q.e.d.
.
q.e.d.
1.11
Reviewing Example 4 with
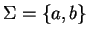 ,
,
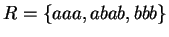 and
and
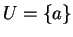 we get the output
we get the output
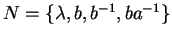 and
and
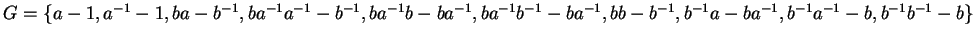 which corresponds to the
non-trivial part of the multiplication table on page
which corresponds to the
non-trivial part of the multiplication table on page ![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/cross_ref_motif.gif) when interpreting the polynomials as described above:
when interpreting the polynomials as described above:
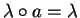 ,
,
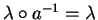 ,
,
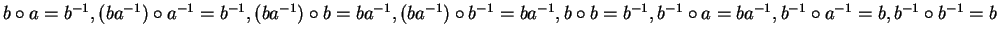 .
Notice that the set G does not give us the trivial relations as
.
Notice that the set G does not give us the trivial relations as
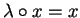 or
or
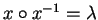 for
for
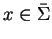 .
They can be applied to make the multiplication table complete.
On the other hand G directly corresponds to the prefix string rewriting system in Example 4
by translating rules
.
They can be applied to make the multiplication table complete.
On the other hand G directly corresponds to the prefix string rewriting system in Example 4
by translating rules
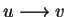 into polynomials u-v and vice versa.
into polynomials u-v and vice versa.



Next: 5. Conclusions
Up: A Note on Nielsen
Previous: 3. Towards Gröbner Bases
| ZCA Home |
Reports |
![]() and
and
![]() ,
respectively.
All ring operations take place in
,
respectively.
All ring operations take place in
![]() .
The following sets are used by the procedure:
.
The following sets are used by the procedure:
, a set of binomials encoding the relators.
, a set of binomials encoding the subgroup generators. [1ex]
; if
then
; else
;
;
; while
do
;
; if
is not prefix reducible by G then
;
;
;
;
;
; endif endwhile endif
![]() added to N the set B contains all border elements
added to N the set B contains all border elements
![]() ,
,
![]() and removing the set of elements
and removing the set of elements
![]() from
N does not destroy the property of being prefix closed.
from
N does not destroy the property of being prefix closed.
![]() is finitely generated and contains a non-trivial normal subgroup then
is finitely generated and contains a non-trivial normal subgroup then
![]() has finite index in
has finite index in
![]() (Proposition 3.11 in [14]).
Since TC terminates in case
(Proposition 3.11 in [14]).
Since TC terminates in case
![]() has finite index in
has finite index in
![]() it remains to show that this is also the
case for procedure EXTENDED TC SIMULATION.
it remains to show that this is also the
case for procedure EXTENDED TC SIMULATION.
![]() is finitely generated
is finitely generated
![]() is also finitely generated (Proposition 3.9 in [14])
and hence has a finite Schreier transversal S.
Then for
is also finitely generated (Proposition 3.9 in [14])
and hence has a finite Schreier transversal S.
Then for ![]() ,
,
![]() and every
and every ![]() there exists just one
there exists just one ![]() such that
such that
![]() .
Since
.
Since
![]() for some
for some
![]() we have
we have
![]() .
The set
.
The set
![]() generates
generates
![]() (compare Chapter 1 in [10]).
But then
(compare Chapter 1 in [10]).
But then
![]() again
is a generating set for
again
is a generating set for
![]() as
as
![]() .
Hence the procedure will terminate at least after checking the candidates
.
Hence the procedure will terminate at least after checking the candidates ![]() for
for ![]() .
q.e.d.
.
q.e.d.
![]() ,
,
![]() and
and
![]() we get the output
we get the output
![]() and
and
![]() which corresponds to the
non-trivial part of the multiplication table on page
which corresponds to the
non-trivial part of the multiplication table on page ![]() when interpreting the polynomials as described above:
when interpreting the polynomials as described above:
![]() ,
,
![]() ,
,
![]() .
Notice that the set G does not give us the trivial relations as
.
Notice that the set G does not give us the trivial relations as
![]() or
or
![]() for
for
![]() .
They can be applied to make the multiplication table complete.
On the other hand G directly corresponds to the prefix string rewriting system in Example 4
by translating rules
.
They can be applied to make the multiplication table complete.
On the other hand G directly corresponds to the prefix string rewriting system in Example 4
by translating rules
![]() into polynomials u-v and vice versa.
into polynomials u-v and vice versa.