


Next: 9. Conclusions
Up: Observations on Coset Enumeration
Previous: 7. Simulating Todd-Coxeter with
8. TC in Monoids
Notice that procedure GENERALIZED TC SIMULATION in fact can also be applied to monoids
by giving as input a string rewriting system
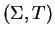 where T no longer needs to contain
the inverse rules.
The question now is, what does the procedure compute in this more general setting?
where T no longer needs to contain
the inverse rules.
The question now is, what does the procedure compute in this more general setting?
Given a finite subset S of a monoid 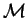 ,
we let
,
we let
 denote
the submonoid generated by S.
A submonoid
denote
the submonoid generated by S.
A submonoid 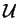 of a monoid
of a monoid 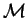 is called finitely generated
if there exists a finite subset S of
is called finitely generated
if there exists a finite subset S of 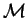 such that
such that
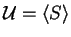 .
.
As in group theory we can define a right congruence as follows:
for
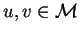 .
But, we can
no longer characterize the submonoid by a special congruence class of this right congruence
as the following example shows:
.
But, we can
no longer characterize the submonoid by a special congruence class of this right congruence
as the following example shows:
Example 5
Let
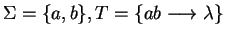
be a string rewriting system presenting
of a monoid
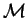
,
the bicyclic monoid.
Let
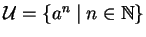
be the submonoid of
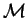
generated by
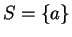
.
For the right congruence class of
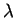
we find
![$[ \lambda ]_{\sim_\mathcal{U}} = \{ \lambda \}$](img173.gif)
,
i.e. even
![$a \not\in [ \lambda ]_{\sim_\mathcal{U}}$](img174.gif)
,
while
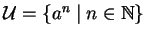
.
So when defining ``cosets'' of submonoids in monoids we meet the difficulty that
they no longer have such nice properties as cosets of subgroups in groups have.
In [12] Neumann gives a different structure which is as close as possible
with respect to the desired properties:
Instead of adopting the analogue of a single coset of a subgroup in a group, he looks
at the set of all cosets:
Given a right congruence on monoids, i.e. an equivalence relation that admits right
multiplication by elements of the monoid, the equivalence classes are called blocks.
If B is such a block, then the elements
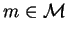 such that
such that
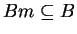 form a submonoid
of
form a submonoid
of 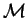 called the fixing submonoid of B.
Different non-void fixing submonoids that arise from the blocks of a right congruence can
then be considered as conjugate.
called the fixing submonoid of B.
Different non-void fixing submonoids that arise from the blocks of a right congruence can
then be considered as conjugate.
Now starting with a submonoid 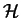 of
of 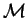 we are looking for the least right congruence that
contains
we are looking for the least right congruence that
contains 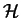 in a block: then
in a block: then 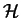 will be contained in the fixing submonoid of that block7.
This is the nearest one can get to ``cosets'' of
will be contained in the fixing submonoid of that block7.
This is the nearest one can get to ``cosets'' of 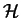 in
in 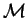 .
.
We can define the block containing 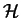 ,
called
,
called
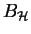 ,
recursively as follows:
,
recursively as follows:
Of course if 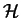 is a subgroup of a group
is a subgroup of a group 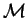 ,
then
,
then
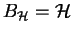 as
as
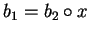 implies
implies
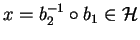 .
.
Notice that when in defining Bi, if some x are used in extending Bi-1
because there are
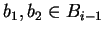 such that
such that
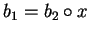 ,
then
,
then 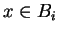 as well since we have
as well since we have
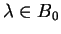 .
.
Reviewing the case of the bicyclic monoid in Example 5 we get
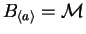 since for
since for
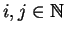 we have
we have
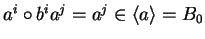 and hence
and hence
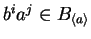 .
Procedure GENERALIZED TC SIMULATION computes the sets
.
Procedure GENERALIZED TC SIMULATION computes the sets
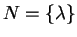 and
and
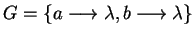 .
On the other hand, if we look at the submonoid generated by b we get
.
On the other hand, if we look at the submonoid generated by b we get
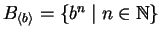 and procedure GENERALIZED TC SIMULATION
computes the infinite sets
and procedure GENERALIZED TC SIMULATION
computes the infinite sets
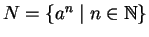 and
and
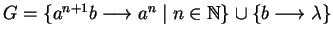 .
.
In order to link for some generating set S the block
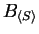 to procedure
GENERALIZED TC SIMULATION, we need the algebraic structure of one-sided ideals in monoid rings.
It is easy to show that there is a one to one correspondence between the congruences generated by
sets of rules
to procedure
GENERALIZED TC SIMULATION, we need the algebraic structure of one-sided ideals in monoid rings.
It is easy to show that there is a one to one correspondence between the congruences generated by
sets of rules
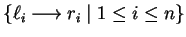 on
on 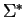 and the congruences of (one-sided) ideals
generated by sets of binomials
and the congruences of (one-sided) ideals
generated by sets of binomials
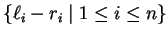 in
in
![$\mathbb{K} [\Sigma^*]$](img201.gif) (see e.g. [8]).
Using this fact, we get the following algebraic characterization of
(see e.g. [8]).
Using this fact, we get the following algebraic characterization of
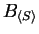 in terms of right ideals in monoid rings.
in terms of right ideals in monoid rings.
Theorem 6
Let
S be a subset of
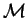
and
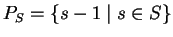
a subset of
![$\mathbb{K} [{\cal M}]$](img203.gif)
associated to
S.
Then the following statements are equivalent for
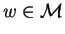
:
- (1)
-
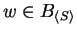 .
.
- (2)
-
![$w- 1 \in {\sf ideal}_{r}^{\mathbb{K} [{\cal M}]}(P_S)$](img206.gif) .
.
Exploiting the connections between string rewriting systems
and special binomial ideal bases, it follows that on termination
the set G computed by
procedure GENERALIZED TC SIMULATION corresponds to a prefix Gröbner basis
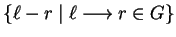 of the right ideal
generated by the set PS in
of the right ideal
generated by the set PS in
![$\mathbb{K} [{\cal M}]$](img203.gif) where
where 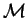 is the monoid presented by
the string rewriting system
is the monoid presented by
the string rewriting system
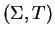 (see [13,8] for more details):
(see [13,8] for more details):
Corollary 7
For
S a subset of
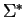
let
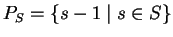
and for
T let
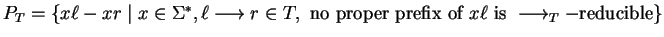
.
Then the following statements are equivalent:
- (1)
-
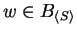 .
.
- (2)
-
![$w- 1 \in {\sf ideal}_{r}^{\mathbb{K} [\Sigma^*]}(P_S \cup P_T)$](img209.gif) .
.
Moreover, if procedure G
ENERALIZED T
C S
IMULATION terminates on input
S and
T with output
G, then
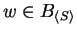
if and only if
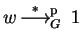
.



Next: 9. Conclusions
Up: Observations on Coset Enumeration
Previous: 7. Simulating Todd-Coxeter with
| ZCA Home |
Reports |
![]() where T no longer needs to contain
the inverse rules.
The question now is, what does the procedure compute in this more general setting?
where T no longer needs to contain
the inverse rules.
The question now is, what does the procedure compute in this more general setting?
![]() ,
we let
,
we let
![]() denote
the submonoid generated by S.
A submonoid
denote
the submonoid generated by S.
A submonoid ![]() of a monoid
of a monoid ![]() is called finitely generated
if there exists a finite subset S of
is called finitely generated
if there exists a finite subset S of ![]() such that
such that
![]() .
.
![]() of
of ![]() we are looking for the least right congruence that
contains
we are looking for the least right congruence that
contains ![]() in a block: then
in a block: then ![]() will be contained in the fixing submonoid of that block7.
This is the nearest one can get to ``cosets'' of
will be contained in the fixing submonoid of that block7.
This is the nearest one can get to ``cosets'' of ![]() in
in ![]() .
.
![]() ,
called
,
called
![]() ,
recursively as follows:
,
recursively as follows:
![]() such that
such that
![]() ,
then
,
then ![]() as well since we have
as well since we have
![]() .
.
![]() since for
since for
![]() we have
we have
![]() and hence
and hence
![]() .
Procedure GENERALIZED TC SIMULATION computes the sets
.
Procedure GENERALIZED TC SIMULATION computes the sets
![]() and
and
![]() .
On the other hand, if we look at the submonoid generated by b we get
.
On the other hand, if we look at the submonoid generated by b we get
![]() and procedure GENERALIZED TC SIMULATION
computes the infinite sets
and procedure GENERALIZED TC SIMULATION
computes the infinite sets
![]() and
and
![]() .
.
![]() to procedure
GENERALIZED TC SIMULATION, we need the algebraic structure of one-sided ideals in monoid rings.
It is easy to show that there is a one to one correspondence between the congruences generated by
sets of rules
to procedure
GENERALIZED TC SIMULATION, we need the algebraic structure of one-sided ideals in monoid rings.
It is easy to show that there is a one to one correspondence between the congruences generated by
sets of rules
![]() on
on ![]() and the congruences of (one-sided) ideals
generated by sets of binomials
and the congruences of (one-sided) ideals
generated by sets of binomials
![]() in
in
![]() (see e.g. [8]).
Using this fact, we get the following algebraic characterization of
(see e.g. [8]).
Using this fact, we get the following algebraic characterization of
![]() in terms of right ideals in monoid rings.
in terms of right ideals in monoid rings.