Now given a subgroup ![]() of
of ![]() for
for
![]() we can
study the cosets
we can
study the cosets
![]() of
of ![]() in
in
![]() .
Since for
.
Since for
![]() either
either
![]() or
or
![]() the group
the group ![]() is a disjoint union of cosets and the number of different
cosets is called the
index
is a disjoint union of cosets and the number of different
cosets is called the
index
![]() of
of ![]() in
in ![]() .
We know that if
.
We know that if ![]() is generated by a set
is generated by a set
![]() the
index of
the
index of ![]() in
in ![]() is the same as the index of the
subgroup
is the same as the index of the
subgroup ![]() generated by
generated by ![]() in
in ![]() .
While it is undecidable whether a subgroup has finite index in a group, coset
enumeration attempts to verify
whether the index is finite by enumerating (potential) cosets and their
multiplication table.
Detailed descriptions of TC procedures can be found e. g. in
[16,1,8,3,15].
.
While it is undecidable whether a subgroup has finite index in a group, coset
enumeration attempts to verify
whether the index is finite by enumerating (potential) cosets and their
multiplication table.
Detailed descriptions of TC procedures can be found e. g. in
[16,1,8,3,15].
In [11] Procedure 1
(see page ![]() )
was presented which simulates the Todd-Coxeter procedure to enumerate cosets
using th ecomputation of prefix Gröbner bases in free group rings
(see [7]).
Besides the sets
)
was presented which simulates the Todd-Coxeter procedure to enumerate cosets
using th ecomputation of prefix Gröbner bases in free group rings
(see [7]).
Besides the sets ![]() and
and ![]() which contain the encoded relators and
subgroup relators, respectively, we have three sets.
First of all,
which contain the encoded relators and
subgroup relators, respectively, we have three sets.
First of all, ![]() which contains the potential coset representatives of the
subgroup generated.
Next,
which contains the potential coset representatives of the
subgroup generated.
Next, ![]() which represents the multiplication table obtained so far and is used
to decide whether or not elements of
which represents the multiplication table obtained so far and is used
to decide whether or not elements of ![]() are indeed coset representatives or
not.
The set
are indeed coset representatives or
not.
The set ![]() serves as a test set for possible coset representatives.
Elements from this set which are not prefix reducible are added to the set
serves as a test set for possible coset representatives.
Elements from this set which are not prefix reducible are added to the set ![]() during the enumeration process.
A detailed description of the meaning of the sets and of the procedure can be
found in [11].
during the enumeration process.
A detailed description of the meaning of the sets and of the procedure can be
found in [11].
While this approach is based on the idea of computing the index of the subgroup
![]() generated by
generated by ![]() in
in ![]() and hence uses Gröbner
basis techniques in
and hence uses Gröbner
basis techniques in
![]() , a splitting of the relations
, a splitting of the relations ![]() can lead
to new enumeration procedures
can lead
to new enumeration procedures ![]() .
For
.
For
![]() where either
where either ![]() is complete or can be finitely
completed to
is complete or can be finitely
completed to
![]() , let
, let ![]() be the group presented by
be the group presented by
![]() , respectively
, respectively
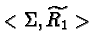 .
Then in a similar fashion we can try to compute the index of the subgroup
.
Then in a similar fashion we can try to compute the index of the subgroup
![]() generated by
generated by ![]() in
in ![]() which is of
course again
which is of
course again
![]() .
The resulting procedure is nearly identical with the original procedure
extended_todd_coxeter_simulation on input
.
The resulting procedure is nearly identical with the original procedure
extended_todd_coxeter_simulation on input ![]() and
and ![]() except that now the computation takes place in
except that now the computation takes place in
![]() and
we have to be more careful in choosing
and
we have to be more careful in choosing ![]() to ensure fairness.
to ensure fairness.
In [10] the possibility of moving relators from the set of relators
generating the group to the free group was studied.
Let the free group be given as
![]() , were
, were
![]() .
Let the relators be given by
.
Let the relators be given by ![]() .
If one of the relators has the form
.
If one of the relators has the form
![]() then we can remove this relator from
then we can remove this relator from ![]() and add it to
and add it to ![]() .
The latter is then completed with respect to the ordering required
using the Knuth-Bendix completion procedure which is this case is always
terminating.
We thus get
.
The latter is then completed with respect to the ordering required
using the Knuth-Bendix completion procedure which is this case is always
terminating.
We thus get ![]() the completed set of rules and
the completed set of rules and
![]() .
Using these we can perform coset enumeration as before.
Other relators, too, can be moved provided a finite and convergent presentation
for the underlying group exists.
.
Using these we can perform coset enumeration as before.
Other relators, too, can be moved provided a finite and convergent presentation
for the underlying group exists.
The original procedure extended_todd_coxeter_simulation was implemented in MRC 1.2 (see [13]) and examples known from the literature (see [1,3]) were computed. Soon it was clear that the original version is far too slow to be of any use except for very small examples. This is not surprising as the Gröbner basis computation which is performed after each new coset element added is quite costly (see also Section 3.3 for a comparison to known methods for coset enumeration).
Thus, different frameworks and strategies have been developed in order to find
out whether the coset enumeration process described is useful compared to
currently known procedures and strategies.
Due to implementational reasons time and space requirements are much higher
for our implementation compared to available implementations of the
Todd-Coxeter-procedure.
First of all, in MRC 1.2 cosets are represented by words, not by numbers,
which requires more space for large examples.
Second, the coefficients are elements of ![]() while they can take the
values
while they can take the
values ![]() only.
Third, since MRC 1.2 handles polynomials, we are encoding relators as
polynomials while using binomials would be sufficient.
Changing the domain of the coefficients and using binomials reduced time
and space requirements drastically.
only.
Third, since MRC 1.2 handles polynomials, we are encoding relators as
polynomials while using binomials would be sufficient.
Changing the domain of the coefficients and using binomials reduced time
and space requirements drastically.
However, more important to us is whether our system can compete with respect to the crucial numbers of Todd-Coxeter-Enumeration: the maximal number of cosets defined during the enumeration process and the total number of cosets defined. Since the enumeration is performed in a different algebraic structure, new parameters play an important role and might help to study cosets from a different point of view.
All frameworks and strategies presented here can as well be used for monoids as for free and general groups (compare [9]).