


Next: 4. The Algorithm
Up: 3. The Extension of
Previous: 3.2 Regular Extensions
3.3 Non-regular Extensions
Assume 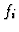 to be an arbitrary element in
to be an arbitrary element in
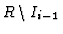 .
Let
.
Let 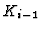 be again a free resolution of
be again a free resolution of 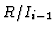 and denote by
and denote by
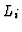 a resolution of
a resolution of 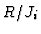 :
:
Lemma 3.6
The multiplication by
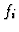
on the
-level induces a homomorphism of
complexes:
PROOF: The situation is the following:
where 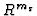 or
or 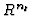 can be zero for
can be zero for 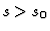 or
or 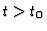 if the
resolutions have different length.
The mapping
if the
resolutions have different length.
The mapping 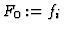 is given. We construct the mappings
is given. We construct the mappings 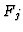 by
induction on
by
induction on 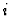 : For
: For
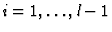 there are mappings
there are mappings
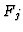 such that
such that
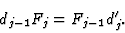 |
(1) |
This condition means that
maps into the kernel of
Now, we start with the indices 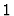 and
and 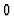 . The image of
. The image of 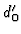 is the
ideal
is the
ideal
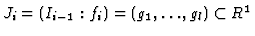 . Thus, a standard
generator
. Thus, a standard
generator 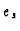 of
of 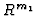 is mapped into
is mapped into 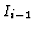 by
by 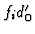 .
We chose a representative
.
We chose a representative
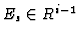 of
of
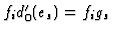 as
an element of
as
an element of 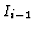 and define the map
and define the map 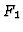 by
by 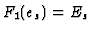 .
Then
.
Then
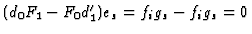 as required.
as required.
Assume 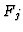 to be constructed. Let
to be constructed. Let 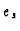 be a standard generator of
be a standard generator of
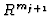 . From
. From
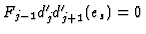 we deduce
we deduce
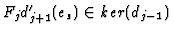 .
Thus, we can chose again a representative
.
Thus, we can chose again a representative 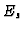 of
of
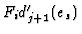 in
in
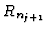 and we define
and we define 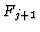 by
by
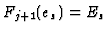 . The equation
(1) follows as in the beginning of the induction.
. The equation
(1) follows as in the beginning of the induction.
Proposition 3.7
The diagram
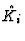
constructed form the homomorphism
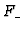
by
reversing the sign of every second map
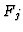
:
constitutes a double complex the total complex of which is a resolution
of
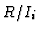
.
PROOF: The first assertion follows from the construction in Lemma
3.6. The second follows again from the spectral sequence
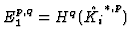 converging to the homology of the total
complex. For a fixed
converging to the homology of the total
complex. For a fixed 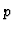 the homology of
the homology of
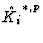 is concentrated
in the zeroth term and
is concentrated
in the zeroth term and
The map in the middle is the multiplication by 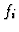 and, consequently, a
monomorphism. Thus, this complex is a resolution of
and, consequently, a
monomorphism. Thus, this complex is a resolution of 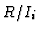 and the second
statement follows.
and the second
statement follows.
REMARK:For an 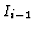 -regular generator
-regular generator 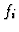 the upper resolution
the upper resolution 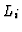 could be
chosen as identical copy of the lower
could be
chosen as identical copy of the lower 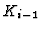 and, hence, the double
complex
and, hence, the double
complex 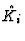 is the natural generalization of the Koszul complex.
is the natural generalization of the Koszul complex.
Note, that the whole construction works over arbitrary rings: The only assumption
is the existence of the free resolutions 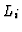 and
and 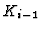 .
.
Definition 3.8
The total complex associated to
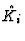
is denoted by
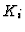
and is
called the
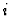
-th subresolution of
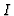
in
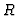
.
Now, asssume that 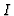 is replaced by an
is replaced by an 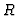 -module
-module
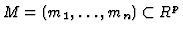 . We define again the
. We define again the 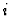 -th extension ideal
by
-th extension ideal
by
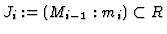 . Here,
. Here, 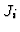 and
and 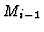 are
non-compatible objects. Therefore, there is no concept analogously to the
are
non-compatible objects. Therefore, there is no concept analogously to the
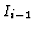 -regularity in the ideal case. Nevertheless, the non-regular
extension of a resolution applies, too.
-regularity in the ideal case. Nevertheless, the non-regular
extension of a resolution applies, too.
Theorem 1
Let
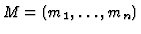
be a module (or an ideal) in
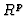
(or
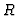
resp.). A resolution of M could be computed from a sequence
of resolutions of the extension ideals
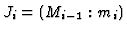
for
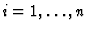
.
REMARK:The resolution constructed via Proposition 3.7 is not minimal
in general: Going back to the proof of Lemma 3.6 we see that
a chosen representation 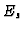 of
of
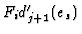 can contain absolute
entries for certain components.
can contain absolute
entries for certain components.
EXAMPLE: Let us consider
![$I=(x^2,y^2,xy)\subset k[x,y]$](img91.gif) . We start with
. We start with
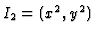 .
. 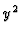 is regular over
is regular over 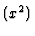 and a resolution of
and a resolution of 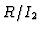 is given by the usual Koszul complex:
is given by the usual Koszul complex:
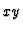 is a zero divisor in
is a zero divisor in 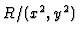 and we obtain
and we obtain 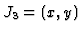 .
Again the Koszul complex is a resolution of
.
Again the Koszul complex is a resolution of 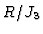 .
.
Now 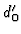 sends
sends 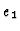 to
to 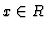 and
and
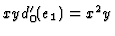 has a representation
by
has a representation
by 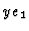 in the lower
in the lower 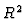 . A representation for
. A representation for
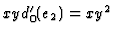 is
given by
is
given by 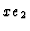 . Thus, we define
. Thus, we define 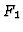 by
by 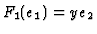 and
and
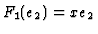 .
.
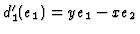 by definition of the Koszul complex. We conclude
by definition of the Koszul complex. We conclude
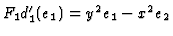 which is just the image of
which is just the image of 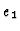 under
under
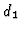 in the lower Koszul complex. Hence,
in the lower Koszul complex. Hence, 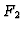 is defined by
is defined by 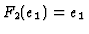 .
.
We see that the total complex 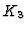 of the double complex
of the double complex 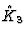 contains absolute entries, i.e., it is not minimal. Indeed, this
property reflects the fact that the syzygy
contains absolute entries, i.e., it is not minimal. Indeed, this
property reflects the fact that the syzygy 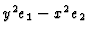 of
of 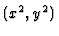 is not a minimal generator of
is not a minimal generator of



Next: 4. The Algorithm
Up: 3. The Extension of
Previous: 3.2 Regular Extensions
| ZCA Home |
Reports |
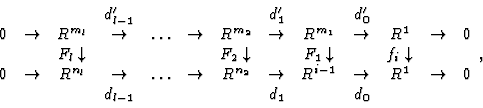
![]() and
and ![]() . The image of
. The image of ![]() is the
ideal
is the
ideal
![]() . Thus, a standard
generator
. Thus, a standard
generator ![]() of
of ![]() is mapped into
is mapped into ![]() by
by ![]() .
We chose a representative
.
We chose a representative
![]() of
of
![]() as
an element of
as
an element of ![]() and define the map
and define the map ![]() by
by ![]() .
Then
.
Then
![]() as required.
as required.
![]() to be constructed. Let
to be constructed. Let ![]() be a standard generator of
be a standard generator of
![]() . From
. From
![]() we deduce
we deduce
![]() .
Thus, we can chose again a representative
.
Thus, we can chose again a representative ![]() of
of
![]() in
in
![]() and we define
and we define ![]() by
by
![]() . The equation
(1) follows as in the beginning of the induction.
. The equation
(1) follows as in the beginning of the induction.![]()
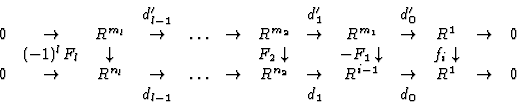
![]() and
and ![]() .
.
![]() is replaced by an
is replaced by an ![]() -module
-module
![]() . We define again the
. We define again the ![]() -th extension ideal
by
-th extension ideal
by
![]() . Here,
. Here, ![]() and
and ![]() are
non-compatible objects. Therefore, there is no concept analogously to the
are
non-compatible objects. Therefore, there is no concept analogously to the
![]() -regularity in the ideal case. Nevertheless, the non-regular
extension of a resolution applies, too.
-regularity in the ideal case. Nevertheless, the non-regular
extension of a resolution applies, too.
![]() sends
sends ![]() to
to ![]() and
and
![]() has a representation
by
has a representation
by ![]() in the lower
in the lower ![]() . A representation for
. A representation for
![]() is
given by
is
given by ![]() . Thus, we define
. Thus, we define ![]() by
by ![]() and
and
![]() .
.
![]() by definition of the Koszul complex. We conclude
by definition of the Koszul complex. We conclude
![]() which is just the image of
which is just the image of ![]() under
under
![]() in the lower Koszul complex. Hence,
in the lower Koszul complex. Hence, ![]() is defined by
is defined by ![]() .
.
![]() of the double complex
of the double complex ![]() contains absolute entries, i.e., it is not minimal. Indeed, this
property reflects the fact that the syzygy
contains absolute entries, i.e., it is not minimal. Indeed, this
property reflects the fact that the syzygy ![]() of
of ![]() is not a minimal generator of
is not a minimal generator of