Consider a singularity ![]() given by power series
given by power series
![]() . The idea of deformation theory is to
perturb the defining functions, that is to consider power series
. The idea of deformation theory is to
perturb the defining functions, that is to consider power series
![]()
![]() with
with
![]() , where
, where ![]() may be considered
as a small parameter of a parameter space
may be considered
as a small parameter of a parameter space ![]() (containing 0).
(containing 0).
For ![]() the power series
the power series
![]() define a singularity
define a singularity
![]() , which is a perturbation of
, which is a perturbation of ![]() for
for ![]() close to 0. It
may be hoped that
close to 0. It
may be hoped that ![]() is simpler than
is simpler than ![]() but still contains enough
information about
but still contains enough
information about ![]() . For this hope to be fulfilled, it is, however,
necessary to restrict the possible perturbations of the equations to
flat perturbations, which are called deformations.
. For this hope to be fulfilled, it is, however,
necessary to restrict the possible perturbations of the equations to
flat perturbations, which are called deformations.
Grothendieck's criterion of flatness states that the perturbation given by the
![]() is flat if and only if any relation between the
is flat if and only if any relation between the ![]() , say
, say
There exists the notion of a semi-universal
deformation of ![]() which contains essentially all information about all
deformations of
which contains essentially all information about all
deformations of ![]() .
.
For an isolated hypersurface singularity
![]() the
semi-universal deformation is given by
the
semi-universal deformation is given by
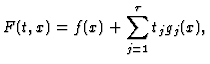
To compute
![]() we only need to compute a standard basis of the
ideal
we only need to compute a standard basis of the
ideal
![]() with respect to a local ordering and then compute a
basis of
with respect to a local ordering and then compute a
basis of ![]() modulo the leading monomials of the standard basis. For
complete intersections we have similar formulas.
modulo the leading monomials of the standard basis. For
complete intersections we have similar formulas.
For non-hypersurface singularities, the semi-universal deformation is much more complicated and up to now no finite algorithm is known in general. However, there exists an algorithm to compute this deformation up to arbitrary high order cf. Ll,Ma1, which is implemented in SINGULAR.
As an example we calculate the base space of the semi-universal deformation
of the normal surface singularity, being the cone over the rational normal
curve ![]() of degree 4, parametrised by
of degree 4, parametrised by
![]() .
.
Homogeneous equations for the cone over ![]() are given by the
are given by the
![]() -minors of the matrix:
-minors of the matrix:
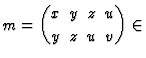 Mat
MatSINGULAR commands for computing the semi-universal deformation:
LIB "deform.lib"; ring r = 0,(x,y,z,u,v),ds; matrix m[2][4] = x,y,z,u,y,z,u,v; ideal f = minor(m,2); versal(f); setring Px; Fs; ==> Fs[1,1]=-u2+zv+Bu+Dv ==> Fs[1,2]=-zu+yv-Au+Du ==> Fs[1,3]=-yu+xv+Cu+Dz ==> Fs[1,4]=z2-yu+Az+By ==> Fs[1,5]=yz-xu+Bx-Cz ==> Fs[1,6]=-y2+xz+Ax+Cy Js; ==> Js[1,1]=BD ==> Js[1,2]=AD-D2 ==> Js[1,3]=-CD |
The ideal
![]() defines the
required base space which consists of a 3-dimensional component
defines the
required base space which consists of a 3-dimensional component ![]() and a
transversal 1-dimensional component
and a
transversal 1-dimensional component
![]() . This was the first
example, found by Pinkham, of a base space of a normal surface having several
components of different dimensions.
. This was the first
example, found by Pinkham, of a base space of a normal surface having several
components of different dimensions.
The full versal deformation is given by the map (Fs and Js as
above)
Although, in general, the equations for the versal deformation are formal power series, in many cases of interest (as in the example above) the algorithm terminates and the resulting ideals are polynomial.
Ingredients for the semi-universal deformation algorithm: