Let
![]() be a convergent power series (in practice a
polynomial) with isolated singularity at 0 and
be a convergent power series (in practice a
polynomial) with isolated singularity at 0 and
![]() the Milnor number of
the Milnor number of ![]() .
.
Then ![]() defines in an
defines in an
![]() -ball
-ball
![]() around 0 a
holomorphic function to
around 0 a
holomorphic function to
![]() ,
,
![]() .
.
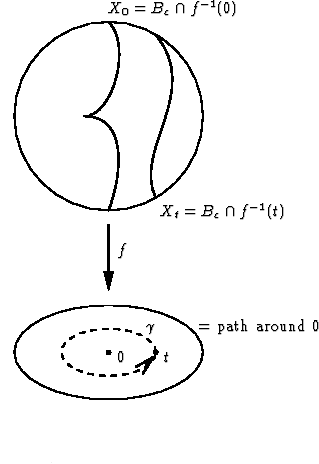
The simple, counterclockwise path ![]() in
in
![]() around 0 induces a
around 0 induces a
![]() -diffeomorphism of
-diffeomorphism of
![]() (as indicated in the
figure) and an automorphism of the singular cohomology group
(as indicated in the
figure) and an automorphism of the singular cohomology group
![]() which is, by a theorem of Milnor, a
which is, by a theorem of Milnor, a ![]() -dimensional
-dimensional
![]() -vector
space. This automorphism
-vector
space. This automorphism
|
The first important theorem is the
Monodromy theorem (Deligne 1970, Brieskorn 1971): The
eigenvalues of ![]() are roots of unity, that is, we have
are roots of unity, that is, we have
Hence, we are left with the problem of computing the Jordan normal form of
![]() .
.
It is not at all clear that the purely topological definition of ![]() allows an
algebraic and computable interpretation. The first hint in this direction is
that we can compute
allows an
algebraic and computable interpretation. The first hint in this direction is
that we can compute
![]() , according to Milnor's theorem,
algebraically by the formula for
, according to Milnor's theorem,
algebraically by the formula for ![]() given above.
given above.
Since ![]() is a complex Stein manifold, its complex cohomology
can be computed, via the holomorphic de Rham theorem, with holomorphic
differential forms, which is the starting point for computing the monodromy.
is a complex Stein manifold, its complex cohomology
can be computed, via the holomorphic de Rham theorem, with holomorphic
differential forms, which is the starting point for computing the monodromy.
To cut a long story short, we just mention, cf. Br,Gre1
that
We define the local Gauß-Manin connection of ![]() as
as
Note that
![]() , that is,
, that is,
![]() has a pole at 0. Tensoring with
has a pole at 0. Tensoring with
![]() , the quotient field of
, the quotient field of
![]() , we can extend
, we can extend
![]() to a meromorphic connection
to a meromorphic connection
With respect to a basis
![]() of
of
![]() we
have
we
have
![]() and,
for any
and,
for any
![]() ,
,
![]() .
Hence, the kernel of
.
Hence, the kernel of
![]() , together with a basis of
, together with a basis of
![]() , is the same as the solutions of the system of rank
, is the same as the solutions of the system of rank ![]() of ordinary differential equations
of ordinary differential equations
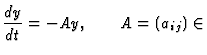 Mat
Mat
Fundamental fact (Brieskorn, 1971): The
Picard-Lefschetz monodromy ![]() coincides with the monodromy
coincides with the monodromy
![]() of the Gauß-Manin connection.
of the Gauß-Manin connection.
Brieskorn used this fact to describe in Br the essential steps for an
algorithm to compute the characteristic polynomial of ![]() . Results of Gerard
and Levelt allowed the extension of this algorithm to compute the Jordan
normal form of
. Results of Gerard
and Levelt allowed the extension of this algorithm to compute the Jordan
normal form of ![]() , cf. GL. An early implementation by Nacken in
Maple was not very efficient. Recently, Schu implemented an
improved version in SINGULAR which is able to compute interesting examples.
, cf. GL. An early implementation by Nacken in
Maple was not very efficient. Recently, Schu implemented an
improved version in SINGULAR which is able to compute interesting examples.
The algorithm uses another basic theorem, the
Regularity Theorem (Brieskorn, 1971): The Gauß-Manin
connection has a regular singular point at 0, that is, there exists a
basis of some lattice in
![]() such that the
connection matrix
such that the
connection matrix ![]() has pole of order 1.
has pole of order 1.
Basically, if
![]() has a simple pole,
then
has a simple pole,
then
![]() is the monodromy (this holds if the eigenvalues of
is the monodromy (this holds if the eigenvalues of
![]() do not differ by integers which can be achieved algorithmically).
do not differ by integers which can be achieved algorithmically).
SINGULAR example:
LIB "mondromy.lib"; ring R = 0,(x,y),ds; poly f = x2y2+x6+y6; //example of A'Campo (monodromy is not diagonalisable) matrix M = monodromy(f); print(jordanform(M)); ==> 1/2,1, 0, 0, 0, 0, 0,0,0,0, 0, 0, 0, ==> 0, 1/2,0, 0, 0, 0, 0,0,0,0, 0, 0, 0, ==> 0, 0, 2/3,0, 0, 0, 0,0,0,0, 0, 0, 0, ==> 0, 0, 0, 2/3,0, 0, 0,0,0,0, 0, 0, 0, ==> 0, 0, 0, 0, 5/6,0, 0,0,0,0, 0, 0, 0, ==> 0, 0, 0, 0, 0, 5/6,0,0,0,0, 0, 0, 0, ==> 0, 0, 0, 0, 0, 0, 1,0,0,0, 0, 0, 0, ==> 0, 0, 0, 0, 0, 0, 0,1,0,0, 0, 0, 0, ==> 0, 0, 0, 0, 0, 0, 0,0,1,0, 0, 0, 0, ==> 0, 0, 0, 0, 0, 0, 0,0,0,7/6,0, 0, 0, ==> 0, 0, 0, 0, 0, 0, 0,0,0,0, 7/6,0, 0, ==> 0, 0, 0, 0, 0, 0, 0,0,0,0, 0, 4/3,0, ==> 0, 0, 0, 0, 0, 0, 0,0,0,0, 0, 0, 4/3Ingredients for the monodromy algorithm:
The most expensive parts are certain normal form computations for a local ordering and the linear algebra part because here one has to deal iteratively with matrices with several thousand rows and columns. It turned out that the SINGULAR implementation of modules (considered as sparse matrices) and the Buchberger inter-reduction is sufficiently efficient (though not the best possible) for such tasks.