1. exactness of the Poincaré complex

The first application is a counterexample to a conjectured generalisation of a theorem of Saito which says that, for an isolated hypersurface singularity, the exactness of the Poincaré complex implies that the defining polynomial is, after some analytic coordinate change, weighted homogeneous.

Theorem [Saito1971]:

If $f : {\mathbb{C}}^{n+1} \longrightarrow {\mathbb{C}}$ has an isolated singularity at 0, then the following are equivalent:

1. $X = f^{-1} (0)$ is weighted homogeneous for a suitable choice of coordinates.

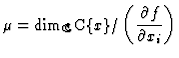2. $\mu = \tau$ where $\mu = \dim_{\mathbb{C}}{\mathbb{C}}\{x\}/\left(\dfrac{\partial f}{\partial x_i}\right)$ is the Milnor number and
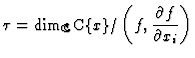   $\tau = \dim_{\mathbb{C}} {\mathbb{C}}\{x\}/\left(f,\dfrac{\partial f}{\partial x_i}\right)$ the Tjurina number.

3. The holomorphic Poincaré complex
   $$0 \longrightarrow {\mathbb{C}}\longrightarrow {\mathcal O}_X \ove... ... \Omega^2_X \longrightarrow \dots \longrightarrow \Omega^n_X \longrightarrow 0$$
   is exact.

A natural problem is whether the theorem holds also for complete intersections $X = f^{-1} (0)$ with $f = (f_1, \dots, f_k) : {\mathbb{C}}^{n+k} \longrightarrow {\mathbb{C}}^k$. Again we have a Milnor number $\mu$ and a Tjurina number $\tau$,

$$\mu = \sum^k_{i=1} (-1)^{i-1} \dim_{\mathbb{C}}{\mathbb{C}}\{x\}/\lef... ...artial(f_1, \dots, f_i)}{\partial(x_{j_1}, \dots, x_{j_i})}\Biggr\lvert \right)$$

$$\tau = \dim_{\mathbb{C}}{\mathbb{C}}\{x\}^k/\bigl(f_1, \dots, f_k) {\mathbb{C}}\{\underline{x}\}^k + Df ({\mathbb{C}}\{\underline{x}\}^{n+k})\bigr).$$

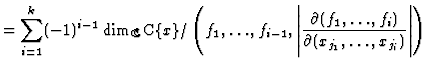Theoretical reduction [Greuel, Martin and Pfister1985]:

If $X$ is a complete intersection of dimension 1, then (1) $\Leftrightarrow$ (2) $\Rightarrow$ (3).
If $k = 2$, then (3) $\Rightarrow$ (2) if $\mu = \dim_{\mathbb{C}}\Omega^2_X - \dim_{\mathbb{C}}\Omega^3_X$ and if $f_1, f_2$ are weighted homogeneous.

PS showed that (3) $\Rightarrow$ (2) does not hold in general:

$$f_1 = xy + z^{\ell-1},\;\; f_2 = xz + y^{k-1} + yz^2 \quad (4 \le \ell \le k,\; k \ge 5)$$

is a counterexample.

The proof uses an implementation of the standard basis algorithm in a forerunner of SINGULAR and goes as follows:

1. Compute $\mu, \dim_{\mathbb{C}}\Omega^2_X, \dim_{\mathbb{C}}\Omega^3_X$ to show that $\Omega^\bullet_X$ is exact;

2. compute $\tau$.
   One obtains $\mu = \tau + 1$, that is, $X$ is not weighted homogeneous.

To do this we must be able to compute standard bases of modules over local rings.

The counterexample was found through a computer search in a list of singularities classified by Wa.