3. curves with maximal number of singularities

Let $C \subset \P ^2_{\mathbb{C}}$ be an irreducible projective curve of degree $d$ and $f(x,y) = 0$ a local equation for the germ $(C,z)$. Let $\mu(C,z) = \dim_{\mathbb{C}}{\mathbb{C}}\{x,y\}/(f_x,f_y)$ be the Milnor number of $C$ at $z$.

Since the genus of $C$, $g(C) = \tfrac{(d-1)(d-2)}{2} - \delta(C)$ is non-negative (where $\delta(C) = \underset{z\in C}{\sum} \delta(C,z)$, $\delta(C,z) = \dim_{\mathbb{C}}\bar{R}/R$, $R = {\mathbb{C}}\{x,y\}/\langle f\rangle$ and $\bar{R}$ the normalisation of $R$), $C$ can have, at most, $(d-1)(d-2)/2$ singularities.

It is a classical and interesting problem, which is still in the centre of theoretical research, to study the variety $V = V_d(S_1, \dots, S_r)$ of (irreducible) curves $C \subset \P ^2_{\mathbb{C}}$ of degree $d$ having exactly $r$ singularities of prescribed (topological or analytical) type $S_1, \dots, S_r$. Among the most important questions are:

• Is $V \not= \emptyset$ (existence problem)?
• Is $V$ irreducible (irreducibility problem)?
• Is $V$ smooth of expected dimension ($T$-smoothness problem)?

A complete answer is only known for nodal curves, that is, for $V_d(r) = V_d(S_1, \dots, S_r)$ with $S_i$ ordinary nodes ($A_1$-singularities):

Severi (1921): $V_d(r) \not= \emptyset$ and $T$-smooth $\Leftrightarrow r \le \tfrac{(d-1)(d-2)}{2}$.

Harris (1985): $V_d(r)$ is irreducible (if $\not= \emptyset$).

Even for cuspidal curves a sufficient and necessary answer to any of the above questions is unknown.

Concerning arbitrary (topological types of) singularities, we have the following existence theorem, which is, with respect to the exponent of $d$, asymptotically optimal.

Theorem: [Greuel, Lossen and Shustin1998,Lossen1999].

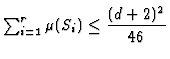$V_d(S_1, \dots, S_r) \not=\emptyset$ if $\sum^r_{i=1} \mu(S_i) \le \dfrac{(d+2)^2}{46}$ and two additional conditions for the five ``worst'' singularities.

In case of only one singularity we have the slightly better sufficient condition for existence,

$$\mu(S_1) \le \dfrac{(d-5)^2}{29}.$$

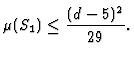
The theorem is just an existence statement, the proof gives no hint how to produce any equation. Having a method for constructing curves of low degree with many singularities, Lossen was able to produce explicit equations. In order to check his construction and improve the results, he made extensive use of SINGULAR to compute standard bases for global as well as for local orderings. One of his examples is the following:

Example: [Lossen1999]    The irreducible curve with affine equation $f(x,y) = 0$,

$$f(x,y) = y^2 - 2y(x^{10} + \dfrac{1}{2} x^{9} y^2 - \dfrac{1}{8} x^{8} y^4 + \dfrac{1}{16} x^{7} y^6 - \dfrac{5}{128} x^{6} y^8 + \dfrac{7}{256} x^5 y^{10}$$

$$- \dfrac{21}{1024} x^4 y^{12} + \dfrac{33}{2048} x^3 y^{14} - \dfrac{429}{32768} x^2 y^{16} + \dfrac{715}{65536} x y^{18}$$

$$- \dfrac{2431}{262144} y^{20}) + x^{20} + x^{19}y^2$$

has degree 21 and an $A_{228}$-singularity $(x^2-y^{229} = 0)$ as its only singularity.

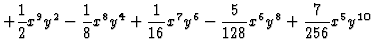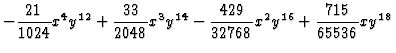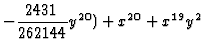In order to verify this, one may proceed, using SINGULAR, as follows:

ring s = 0,(x,y),ds;
poly f = y2-2x10y-x9y3+1/4x8y5-1/8x7y7+5/64x6y9-7/128x5y11+21/512x4y13 
        -33/1024x3y15+429/16384x2y17+x20-715/32768xy19+x19y2+2431/131072y21;
matrix Hess = jacob(jacob(f));         //the Hessian matrix of f
print(subst(subst(Hess,x,0),y,0));     //the Hessian matrix for x=y=0
==> 0,0,
==> 0,2 
vdim(std(jacob(f)));                  //the Milnor number of f
==> 228

Since the rank of the Hessian at 0 is 1, $f$ has an $A_k$ singularity at 0; it is an $A_{228}$ singularity since the Milnor number is 228. To show that the projective curve $C$ defined by $f$ has no other singularities, we have to show that $C$ has no further singularities in the affine part and no singularity at infinity. The second assertion is easy, the first follows from

$$dim_{\mathbb{C}}(K[x,y]_{\langle x,y\rangle}/\langle$$jacob$$(f),f\rangle = \dim_{\mathbb{C}}(K[x,y]/\langle$$   jacob$$(f),f\rangle,$$

confirmed by SINGULAR:

vdim(std(jacob(f)+f));
==> 228                     //multiplicity of Sing(C) at 0 (local ordering)
ring r = 0,(x,y),dp;
poly f = fetch(s,f);
vdim(std(jacob(f)+f));
==> 228                     //multiplicity of Sing(C)      (global ordering)