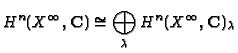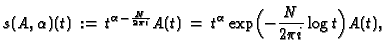Next: V-filtration
Up: V-filtration and spectral numbers
Previous: Milnor fibration
There is a natural action of the fundamental group
 ,
,
 , on
, on
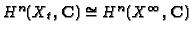 .
A positively oriented generator of
.
A positively oriented generator of
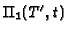 operates via the
monodromy operator
operates via the
monodromy operator 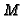 defined by
defined by
for
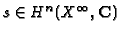 and
and
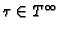 .
Let
.
Let 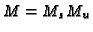 be the decomposition of
be the decomposition of 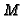 into the semisimple
part
into the semisimple
part 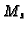 and the unipotent part
and the unipotent part 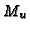 , and set
, and set
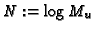 .
By the monodromy theorem [1,24], the eigenvalues of
.
By the monodromy theorem [1,24], the eigenvalues of
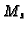 are roots of unity and
are roots of unity and 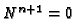 .
Let
be the decomposition of
.
Let
be the decomposition of
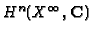 into the generalized
eigenspaces of
into the generalized
eigenspaces of 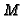 ,
,
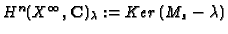 ,
,
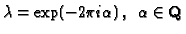 ,
and let
,
and let
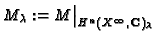 .
For
.
For
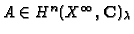 ,
,
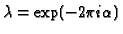 ,
is monodromy invariant and defines a holomorphic section in
,
is monodromy invariant and defines a holomorphic section in 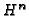 .
The sections
.
The sections
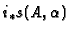 span a
span a
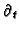 -invariant, finitely
generated, free
-invariant, finitely
generated, free
![$ \mathcal{O}_T[t^{-1}]$](img609.gif) -submodule
-submodule
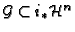 of rank
of rank 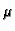 . Note that
the direct image sheaf
. Note that
the direct image sheaf
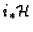 is in general not finitely
generated. The Gauß-Manin connection is the regular
is in general not finitely
generated. The Gauß-Manin connection is the regular
![$ {\mathbf{C}\{t\}}[\partial_t]$](img612.gif) -module
-module
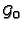 , the stalk of
, the stalk of
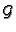 at 0 [1,32].
at 0 [1,32].
Christoph Lossen
2001-03-21
![]() ,
,
![]() , on
, on
![]() .
A positively oriented generator of
.
A positively oriented generator of
![]() operates via the
monodromy operator
operates via the
monodromy operator ![]() defined by
defined by