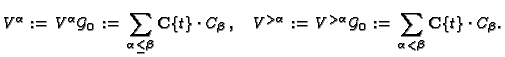Next: Brieskorn lattice
Up: V-filtration and spectral numbers
Previous: Gauß-Manin connection
Since
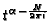 is invertible,
is invertible,
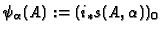 defines an inclusion
defines an inclusion
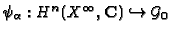 ,
satisfying the relations
,
satisfying the relations
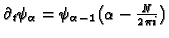 and
and
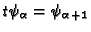 ,
by definition of
,
by definition of
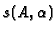 .
This implies
.
This implies
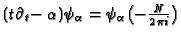 ,
,
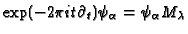 , and the image
, and the image
of
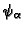 is the generalized
is the generalized 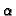 -eigenspace of
-eigenspace of
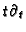 . Moreover,
. Moreover,
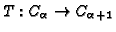 is
bijective, and
is
bijective, and
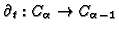 is
bijective for
is
bijective for
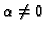 .
The V-filtration
.
The V-filtration 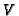 on
on
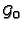 is defined by
is defined by
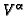 and
and
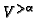 are free
are free
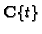 -modules of rank
-modules of rank
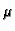 with
with
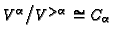 .
.
Christoph Lossen
2001-03-21
![]() is invertible,
is invertible,
![]() defines an inclusion
defines an inclusion
![]() ,
satisfying the relations
,
satisfying the relations
![]() and
and
![]() ,
by definition of
,
by definition of
![]() .
This implies
.
This implies
![]() ,
,
![]() , and the image
, and the image