


Next: Microlocal structure
Up: V-filtration and spectral numbers
Previous: V-filtration
The Brieskorn lattice [1]
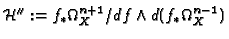 is a free
is a free
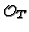 -module of rank
-module of rank 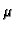 [38].
The Gelfand-Leray form
[38].
The Gelfand-Leray form
defines a map
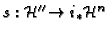 with
image in
with
image in
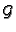 , inducing an isomorphism
, inducing an isomorphism
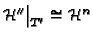 , and satisfying
, and satisfying
![$ \partial_t s\bigl([{d\!\,}
f\!\!\:\wedge\eta]\bigr)=s\bigl([{d\!\,}\eta]\bigr)$](img639.gif) by the Leray residue formula [1].
Since
by the Leray residue formula [1].
Since
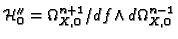 is a torsion free
is a torsion free
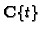 -module,
-module,
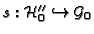 is an inclusion, and we identify
is an inclusion, and we identify
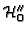 with its image in
with its image in
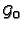 . By a result of [29], we
have
. By a result of [29], we
have
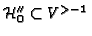 .
.
Christoph Lossen
2001-03-21
![]() is a free
is a free
![]() -module of rank
-module of rank ![]() [38].
The Gelfand-Leray form
[38].
The Gelfand-Leray form