


Next: Summary
Up: Algorithm
Previous: Idea
By the finite determinacy theorem, we may assume that
![$ f\in\mathbf{C}[\boldsymbol{x}]$](img686.gif) ,
,
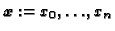 , is a polynomial.
Since
, is a polynomial.
Since
![$ \mathbf{C}[\boldsymbol{x}]_{(\boldsymbol{x})}\subset\mathbf{C}\{\boldsymbol{x}\}$](img688.gif) is faithfully flat and all
data will be defined over
is faithfully flat and all
data will be defined over
![$ \mathbf{C}[\boldsymbol{x}]_{(\boldsymbol{x})}$](img689.gif) , we may replace
, we may replace
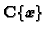 by
by
![$ \mathbf{C}[\boldsymbol{x}]_{(\boldsymbol{x})}$](img689.gif) and, similarly,
and, similarly,
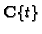 by
by
![$ \mathbf{C}[t]_{(t)}$](img691.gif) and
and
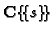 by
by
![$ \mathbf{C}[s]_{(s)}$](img692.gif) for the computation.
With the additional assumption
for the computation.
With the additional assumption
![$ f\in\mathbf{Q}[\boldsymbol{x}]$](img693.gif) , all data will be
defined over
, all data will be
defined over
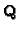 , and we can apply methods of computer algebra.
Using standard basis methods for local rings,
, and we can apply methods of computer algebra.
Using standard basis methods for local rings,
![$ \mathbf{C}[\boldsymbol{x}]_{\langle \boldsymbol{x}\rangle}$](img695.gif) one can compute a monomial
one can compute a monomial
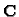 -basis
-basis
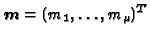 of
of
Since
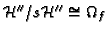 ,
,
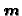 represents a
represents a
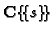 -basis of
-basis of
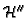 and a
and a
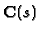 -basis of
-basis of
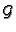 by
Nakayama's lemma.
by
Nakayama's lemma.
The matrix  of
of 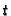 with respect to
with respect to
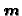 is defined by
is defined by
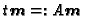 . Since
. Since
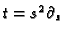 , we obtain for
, we obtain for
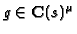
So the action of 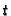 in terms of the
in terms of the
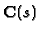 -basis
-basis
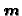 is determined
by the matrix
is determined
by the matrix  by the above formula.
by the above formula.
A reduced normalform with respect to a local monomial
ordering allows to compute the projection to the first summand in
Since
![$ t[\omega]=[f\omega]$](img706.gif) and
and
![$ s^{-1}[{d\!\,}
f\wedge\eta]=\partial_t[{d\!\,} f\wedge\eta]=[{d\!\,}\eta]$](img707.gif) ,
the matrix
,
the matrix  of
of 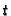 with respect to
with respect to
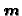 can be computed up to
arbitrarily high order.
can be computed up to
arbitrarily high order.
The basis representation 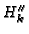 of
of
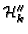 with respect to
with respect to
 defined by
defined by
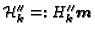 can be computed
inductively by
can be computed
inductively by
Using standard basis methods, one can check if
 and compute a
and compute a
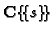 -basis
-basis
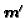 of
of
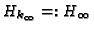 with
Then the matrix
with
Then the matrix 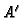 of
of 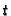 with respect to the
with respect to the
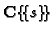 -basis
-basis
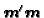 of
of
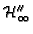 is defined by the formula
is defined by the formula
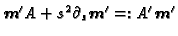 , and
, and
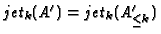 for
for
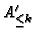 defined by
Hence, the basis representation of
defined by
Hence, the basis representation of
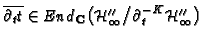
with respect to
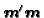 is
is
The basis representation 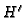 of
of
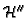 with respect to
with respect to
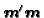 is defined by
is defined by
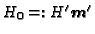 , and
, and
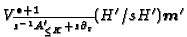 is the basis representation of
is the basis representation of
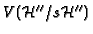 with respect to
with respect to
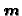 . The matrix of
. The matrix of
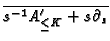 with respect to the
canonical
with respect to the
canonical
 -basis
of
-basis
of
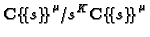 is given by the block matrix
where
is given by the block matrix
where
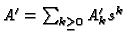 .
Since the eigenvalues of
.
Since the eigenvalues of 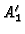 are rational, they can be computed
using univariate factorization over the rational numbers.
Then the V-filtration
are rational, they can be computed
using univariate factorization over the rational numbers.
Then the V-filtration
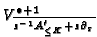 can be computed using methods of linear algebra.
can be computed using methods of linear algebra.



Next: Summary
Up: Algorithm
Previous: Idea
Christoph Lossen
2001-03-21
![]() ,
,
![]() , is a polynomial.
Since
, is a polynomial.
Since
![]() is faithfully flat and all
data will be defined over
is faithfully flat and all
data will be defined over
![]() , we may replace
, we may replace
![]() by
by
![]() and, similarly,
and, similarly,
![]() by
by
![]() and
and
![]() by
by
![]() for the computation.
With the additional assumption
for the computation.
With the additional assumption
![]() , all data will be
defined over
, all data will be
defined over
![]() , and we can apply methods of computer algebra.
Using standard basis methods for local rings,
, and we can apply methods of computer algebra.
Using standard basis methods for local rings,
![]() one can compute a monomial
one can compute a monomial
![]() -basis
-basis
![]() of
of
![]() of
of ![]() with respect to
with respect to
![]() is defined by
is defined by
![]() . Since
. Since
![]() , we obtain for
, we obtain for
![]()
![]() of
of
![]() with respect to
with respect to
![]() defined by
defined by
![]() can be computed
inductively by
can be computed
inductively by
![]() is
is

