


Next: Example
Up: Algorithm
Previous: Computation
Here are the main steps of the algorithm:
- Compute a
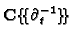 -basis
-basis
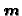 of
of
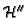 .
.
- For increasing
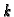 compute successively the lattices
compute successively the lattices
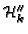 in terms of
in terms of
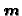 , and
, and 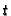 in terms of
in terms of
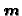 up
to order
up
to order 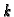 until
until
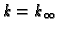 and
and
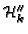 is the
saturation
is the
saturation
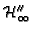 of
of
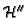 .
.
- Compute a
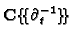 -basis
-basis
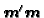 of
of
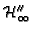 .
.
- Compute
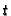 in terms of
in terms of
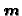 up to order
up to order
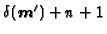 .
.
- Compute
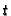 in terms of
in terms of
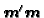 up to order
up to order 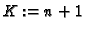 .
.
- Compute
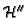 in terms of
in terms of
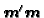 .
.
- Compute the
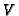 -filtration on
-filtration on
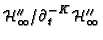 in
terms of
in
terms of
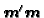 .
.
- Compute the induced
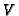 -filtration on
-filtration on
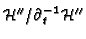 in terms of
in terms of
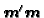 .
.
Christoph Lossen
2001-03-21