


Next: Normalization algorithm
Up: Integral closure of rings
Previous: Ring normalization
Test ideals
It remains to find a test ideal. For this we consider the singular
locus
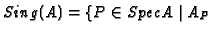
is not regular
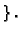
Since every regular local ring is normal,
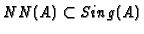 . For general Noetherian rings, however, Sing
. For general Noetherian rings, however, Sing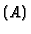 may
not be closed in the Zariski topology. Therefore, we pass to more
special rings.
may
not be closed in the Zariski topology. Therefore, we pass to more
special rings.
Let
![$ S = K[x_1, \dots, x_n]$](img112.gif) and
and 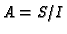 be an affine ring where
be an affine ring where 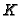 is a perfect field. If
is a perfect field. If  is equidimensional of codimension
is equidimensional of codimension 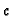 ,
that is, all minimal primes
,
that is, all minimal primes 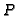 of
of 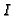 have the same height
have the same height 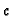 , then
the Jacobian ideal of
, then
the Jacobian ideal of 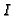 defines Sing
defines Sing . That is, if
. That is, if
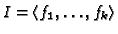 and
and
is the Jacobian ideal of 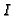 , then Sing
, then Sing
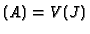 . If, on the
other hand,
. If, on the
other hand,  is not equidimensional, then
is not equidimensional, then 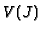 may be strictly
contained in Sing
may be strictly
contained in Sing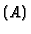 , if we define
, if we define 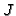 as above with
as above with 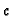 the minimal
height of minimal primes of
the minimal
height of minimal primes of 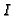 . In this case we need another ideal.
There are several alternatives to compute an ideal
. In this case we need another ideal.
There are several alternatives to compute an ideal  with
with
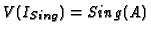 . Either we compute an equidimensional
decomposition
. Either we compute an equidimensional
decomposition
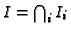 ,
[8,15], of
,
[8,15], of 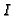 , compute the Jacobian ideal
, compute the Jacobian ideal 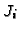 for each equidimensional ideal
for each equidimensional ideal 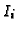 and compute the ideal describing
the intersection of any two equidimensional parts. The same works for
a primary decomposition, [11,8,15])
instead of an equidimensional decomposition.
and compute the ideal describing
the intersection of any two equidimensional parts. The same works for
a primary decomposition, [11,8,15])
instead of an equidimensional decomposition.
We can avoid an equidimensional, resp. primary, decomposition if we
compute the ideal of the non-free locus of the module of Kähler
differentials,
where
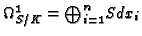 .
.
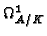 is isomorphic to
is isomorphic to 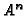 modulo the submodule generated
by the rows of the Jacobian matrix of
modulo the submodule generated
by the rows of the Jacobian matrix of
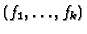 , hence it is
finitely presented by the transpose of the Jacobian matrix.
, hence it is
finitely presented by the transpose of the Jacobian matrix.
For any finitely presented  -module
-module 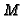 we can compute the non-free
locus
we can compute the non-free
locus
just by Gröbner basis and syzygy computations, cf. [15].
Let  be an ideal defining the singular locus of
be an ideal defining the singular locus of 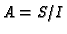 . Since
. Since  is reduced,
is reduced,  contains a non-zerodivisor
of
contains a non-zerodivisor
of  . Indeed, a general linear combination
. Indeed, a general linear combination 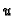 of the generators
of
of the generators
of  will be a non-zerodivisor. Hence,
any radical ideal of
will be a non-zerodivisor. Hence,
any radical ideal of 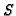 which contains
which contains 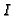 and
and 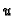 will be a test
ideal for normality. Two extreme choices for test ideals are
will be a test
ideal for normality. Two extreme choices for test ideals are
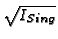 or
or
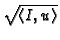 .
.
Since the radical of an ideal in an affine ring can be computed,
[8,25,15], we have all ingredients to compute the normalization
of  .
.
In the remaining part of this section, we describe algorithms to
compute
- the normalization
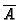 of
of  , that is, we
represent
, that is, we
represent
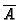 as affine ring and describe the map
as affine ring and describe the map
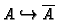 ,
,
- generators for an ideal
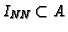 describing the non-normal locus, that is,
describing the non-normal locus, that is,
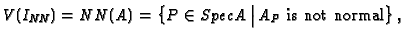
- for any ideal
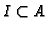 , generators for the integral
closure
, generators for the integral
closure
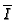 of
of 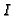 in
in  .
.



Next: Normalization algorithm
Up: Integral closure of rings
Previous: Ring normalization
Christoph Lossen
2001-03-21
![]() and
and ![]() be an affine ring where
be an affine ring where ![]() is a perfect field. If
is a perfect field. If ![]() is equidimensional of codimension
is equidimensional of codimension ![]() ,
that is, all minimal primes
,
that is, all minimal primes ![]() of
of ![]() have the same height
have the same height ![]() , then
the Jacobian ideal of
, then
the Jacobian ideal of ![]() defines Sing
defines Sing![]() . That is, if
. That is, if
![]() and
and
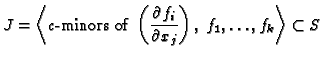
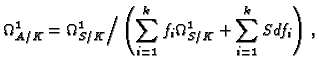
![]() -module
-module ![]() we can compute the non-free
locus
we can compute the non-free
locus
![]() be an ideal defining the singular locus of
be an ideal defining the singular locus of ![]() . Since
. Since ![]() is reduced,
is reduced, ![]() contains a non-zerodivisor
of
contains a non-zerodivisor
of ![]() . Indeed, a general linear combination
. Indeed, a general linear combination ![]() of the generators
of
of the generators
of ![]() will be a non-zerodivisor. Hence,
any radical ideal of
will be a non-zerodivisor. Hence,
any radical ideal of ![]() which contains
which contains ![]() and
and ![]() will be a test
ideal for normality. Two extreme choices for test ideals are
will be a test
ideal for normality. Two extreme choices for test ideals are
![]() or
or
![]() .
.
![]() .
.