


Next: Test ideals
Up: Integral closure of rings
Previous: Integral closure of rings
Let
 be a ring extension and
be a ring extension and
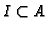 an ideal. Recall that
an ideal. Recall that  is called (strongly)
integral over
is called (strongly)
integral over 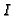 if
if  satisfies a relation
satisfies a relation

with

The set
 is integral over
is integral over  is called the integral closure of
is called the integral closure of 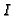 in
in  , it is a
, it is a
 -module, where
-module, where  , the integral closure of
, the integral closure of  in
in  ,
is a ring.
,
is a ring.
We are interested in the two most interesting cases:
Let us consider the normalization first.
Lemma 1.1 (Key-lemma)
Let

be a reduced Noetherian ring and

an
ideal containing a non-zerodivisor
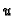
of

. Then there are
natural inclusions of rings
and inclusions

of

-modules.
Here

.
Proof.
If
 , then
, then
 is
independent of the non-zerodivisor
is
independent of the non-zerodivisor 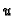 and, hence,
and, hence,
 defines an embedding
The inclusion
defines an embedding
The inclusion
 is given by the multiplication with elements of
is given by the multiplication with elements of  . To see that the
image is contained in
. To see that the
image is contained in
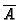 , consider
, consider
 . The characteristic polynomial of
. The characteristic polynomial of
 defines (by Cayley-Hamilton) an integral relation for
defines (by Cayley-Hamilton) an integral relation for
 . To see the last inclusion, consider
. To see the last inclusion, consider
 such that
such that
 ,
and let
,
and let
 ,
,  , be an
integral relation for
, be an
integral relation for  . For a given
. For a given  multiply the
relation for
multiply the
relation for  with
with  . This shows that
. This shows that
 , hence
, hence
 .
.
Since  is normal if and only if the localization
is normal if and only if the localization  is normal
for all
is normal
for all
 , we define the non-normal locus of
, we define the non-normal locus of  as
as

is not normal
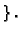
It is easy to see that
 where
where
 is the conductor of
is the conductor of  in
in
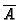 , in particular,
, in particular,  is closed in
is closed in
 . However, since we cannot yet compute
. However, since we cannot yet compute
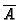 , we
cannot compute
, we
cannot compute 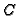 either.
either.
The following proposition is the basis for the algorithm to compute
the normalization as well as for an algorithm to compute an ideal with
zero set  . It is basically due to Grauert and Remmert,
[12].
. It is basically due to Grauert and Remmert,
[12].
Proposition 1.2 (Criterion for normality)
Let

be a reduced Noetherian ring and

an ideal
satisfying
- 1.
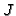 contains a non-zerodivisor of
contains a non-zerodivisor of  ,
,
- 2.
-
 ,
,
- 3.
-
 .
.
Then

if and only if

.
An ideal
 satisfying 1.-3. is called a test
ideal for the normalization.
satisfying 1.-3. is called a test
ideal for the normalization.
Proof.
If
 then
then
 , by Lemma
1.1. For the converse, notice that 3. implies
, by Lemma
1.1. For the converse, notice that 3. implies
 , hence there exists a minimal
, hence there exists a minimal  such that
such that  , that is,
, that is,
 . If
. If  , choose
, choose
 and
and
 such that
such that
 . Since
. Since
 and
and
 we
have
we
have
 and hence, using
2.,
and hence, using
2.,
 , by Lemma 1.1. By
assumption
, by Lemma 1.1. By
assumption
 and, hence,
and, hence,  .
This is a contradiction, and we conclude
.
This is a contradiction, and we conclude  and
and
 .
.
Remark 1.3
As the proof shows, condition 2. can be weakened to
- 2'.
-
 .
.
However, this
cannot be used in practice, since we do not know
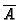
,
while, on the other hand, we can always
pass from
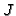
to

without violating the conditions 1 and 3,
and

is computable.
Proof.
This follows from 1.2, 1.1 and the fact that the
operations which define the annihilator are compatible with
localization.
Having a test ideal 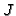 and a non-zerodivisor
and a non-zerodivisor  of
of
 , we can compute
, we can compute  -module generators of
-module generators of
 and
and  -module generators for
-module generators for
 ,
since we can compute ideal quotients using Gröbner
basis methods, cf. [15].
,
since we can compute ideal quotients using Gröbner
basis methods, cf. [15].
Let us describe the ring structure of
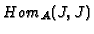 .
For this, let
.
For this, let  ,
,
 be generators of
be generators of
 as
as  -module, and let
-module, and let
 be generators of the module of
syzygies of
be generators of the module of
syzygies of
 . Since
. Since
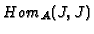 is a ring,
we have
is a ring,
we have
 ,
,
 for certain
for certain
 , the quadratic relations between the
, the quadratic relations between the
 . Define
. Define
![$ Ker\subset A[t_1, \dots, t_s]$](img104.gif) as the ideal
generated by the linear and quadratic relations,
as the ideal
generated by the linear and quadratic relations,
We get an isomorphism
![$ Hom_A(J,J) \cong uJ : J \cong
A[t_1, \dots, t_s]/Ker$](img106.gif) of
of  -algebras, by sending
-algebras, by sending  to
to  .
This presentation is needed to continue the normalization algorithm.
.
This presentation is needed to continue the normalization algorithm.
To compute
 , we only need the
, we only need the  -module
structure of
-module
structure of  .
.



Next: Test ideals
Up: Integral closure of rings
Previous: Integral closure of rings
Christoph Lossen
2001-03-21
![]() be a ring extension and
be a ring extension and
![]() an ideal. Recall that
an ideal. Recall that ![]() is called (strongly)
integral over
is called (strongly)
integral over ![]() if
if ![]() satisfies a relation
satisfies a relation

![]() is normal if and only if the localization
is normal if and only if the localization ![]() is normal
for all
is normal
for all
![]() , we define the non-normal locus of
, we define the non-normal locus of ![]() as
as
![]() . It is basically due to Grauert and Remmert,
[12].
. It is basically due to Grauert and Remmert,
[12].
![]() .
For this, let
.
For this, let ![]() ,
,
![]() be generators of
be generators of
![]() as
as ![]() -module, and let
-module, and let
![]() be generators of the module of
syzygies of
be generators of the module of
syzygies of
![]() . Since
. Since
![]() is a ring,
we have
is a ring,
we have
![]() ,
,
![]() for certain
for certain
![]() , the quadratic relations between the
, the quadratic relations between the
![]() . Define
. Define
![]() as the ideal
generated by the linear and quadratic relations,
as the ideal
generated by the linear and quadratic relations,
![]() , we only need the
, we only need the ![]() -module
structure of
-module
structure of ![]() .
.