


Next: Examples
Up: Integral closure of rings
Previous: Computing the normalization
Let  be a ring,
be a ring,
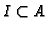 an ideal. We propose an
algorithm to compute
an ideal. We propose an
algorithm to compute
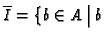 is integral
over
is integral
over 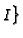 , the integral
closure of
, the integral
closure of 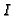 .
.
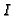 is called integrally closed if and only if
is called integrally closed if and only if
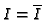 . It is called
normal if
. It is called
normal if
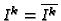 for all
for all 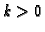 .
Note that
.
Note that
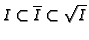 .
We are mainly interested in the case
.
We are mainly interested in the case
![$ A = K[x_1, \dots, x_n]$](img183.gif) .
.
In the following, we describe an algorithm to compute
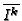 for all
for all 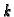 , simultaneously. Consider the Rees
algebra
, simultaneously. Consider the Rees
algebra
![$ \mathcal{R}(I) = \bigoplus_{k \ge 0} I^k t^k \subset
A[t]$](img184.gif) , and let
, and let
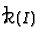 denote the integral closure of
denote the integral closure of
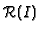 in
in ![$ A[t]$](img187.gif) . Then
. Then
If  is normal, then
is normal, then ![$ A[t]$](img187.gif) is normal and hence, the normalization
of
is normal and hence, the normalization
of
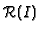 , that is, the integral closure of
, that is, the integral closure of
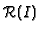 in
in
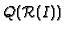 ,
satisfies
Hence, computing the normalization of
,
satisfies
Hence, computing the normalization of
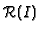 provides the integral
closure of
provides the integral
closure of
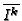 for all
for all 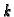 .
.
To be specific, let
![$ A = K[{\boldsymbol{x}}] = K[x_1, \dots, x_n]$](img191.gif) ,
,
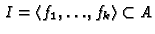 with
with 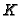 a
perfect field. Then
a
perfect field. Then
where
![$ \varphi : K[{\boldsymbol{x}},{\boldsymbol{U}}] \to K[{\boldsymbol{x}},t]$](img194.gif) maps
maps
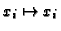 ,
,
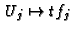 .
.
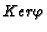 can be computed by eliminating
can be computed by eliminating 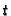 from
that is,
from
that is,
![$ Ker\varphi = J \cap K[{\boldsymbol{x}},{\boldsymbol{U}}]$](img199.gif) .
For the integral closure of
.
For the integral closure of 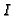 we need to compute
This means that we compute
we need to compute
This means that we compute
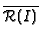 as an affine ring
as an affine ring
![$ K[\boldsymbol{T}]/I'$](img201.gif) and, in each inductive step during the computation of
and, in each inductive step during the computation of
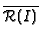 , we also
compute the map from the intermediate ring to
, we also
compute the map from the intermediate ring to
![$ K[{\boldsymbol{x}},t]$](img202.gif) .
.
The algorithm then reads as follows:
- Input
-
![$ f_1, \dots, f_\ell \in K[x_1, \dots,
x_n]$](img203.gif) ,
,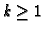 an integer,
an integer,
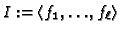 .
.
- Output
- Generators for
![$ \overline{I^k} \subset K[x_1, \dots,
x_n]$](img206.gif) .
.
- Compute the Rees algebra
![$ \mathcal{R}(I) \subset K[{\boldsymbol{x}},t]$](img207.gif) .
.
- Compute the normalization
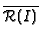 , together with
maps
, together with
maps
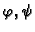 , so that
commutes.
, so that
commutes.
- Determine
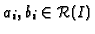 , so that
, so that
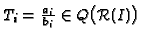 compute
compute
![$ \tfrac{\varphi(a_i)}{\varphi(b_i)}\in K[{\boldsymbol{x}},t]$](img212.gif) (indeed, we
find a universal denominator
(indeed, we
find a universal denominator 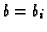 for all
for all 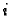 ).
).
- Determine generators
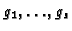 of the
of the
![$ K[\boldsymbol{x}]$](img216.gif) -ideal which is mapped to the component of
-ideal which is mapped to the component of 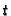 -degree
-degree
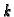 of the subalgebra
of the subalgebra
![$ \psi\bigl(\overline{\mathcal{R}(I)}\bigr) \subset
K[{\boldsymbol{x}},t]$](img217.gif) .
.
- Return
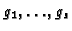 .
.
The algorithms described above are implemented in SINGULAR and
contained in the libraries normal.lib [16]
and reesclos.lib [23] contained in the distribution of
SINGULAR 2.0 [17]. Similar procedures can be used to
compute the conductor ideal of  in
in
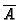 . An
implementation will be available soon.
. An
implementation will be available soon.



Next: Examples
Up: Integral closure of rings
Previous: Computing the normalization
Christoph Lossen
2001-03-21
![]() be a ring,
be a ring,
![]() an ideal. We propose an
algorithm to compute
an ideal. We propose an
algorithm to compute
![]() is integral
over
is integral
over ![]() , the integral
closure of
, the integral
closure of ![]() .
.
![]() is called integrally closed if and only if
is called integrally closed if and only if
![]() . It is called
normal if
. It is called
normal if
![]() for all
for all ![]() .
Note that
.
Note that
![]() .
We are mainly interested in the case
.
We are mainly interested in the case
![]() .
.
![]() for all
for all ![]() , simultaneously. Consider the Rees
algebra
, simultaneously. Consider the Rees
algebra
![]() , and let
, and let
![]() denote the integral closure of
denote the integral closure of
![]() in
in ![]() . Then
. Then
![]() ,
,
![]() with
with ![]() a
perfect field. Then
a
perfect field. Then
![$\displaystyle \UseComputerModernTips\xymatrix @C=0pt@R=2pt{
& \mathcal{R}(I) &\...
...upset &\overline{\mathcal{R}(I)} & =\, K[T_1, \dots,
T_s]/I'\,. \ar[uuurrr]
}
$](img200.gif)
![$\displaystyle \UseComputerModernTips\xymatrix @C=1pt@R=6pt{
& \mathcal{R}(I) \a...
...mathcal{R}(I)} \ar@{=}[rrr] &&&
K[T_1, \dots, T_s]/J\ar@{^{(}->}[uu]_-{\psi}
}
$](img209.gif)
![]() in
in
![]() . An
implementation will be available soon.
. An
implementation will be available soon.