


Next: Integral closure algorithm
Up: Normalization algorithm
Previous: Computing the non-normal locus
The idea for computing the normalization of 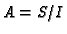 is as
follows:
is as
follows:
For performance reasons we do not look for a non-zerodivisor in 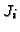 but choose any non-zero element
but choose any non-zero element 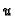 . If
. If 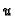 is a zerodivisor then it
gives a splitting of the ring which makes the subsequent computations
easier.
is a zerodivisor then it
gives a splitting of the ring which makes the subsequent computations
easier.
We obtain the following (highly recursive) algorithm for computing the
normalization:
- Input
-
![$ f_1, \dots, f_k \in S=K[x_1, \dots, x_n]$](img141.gif) ,
,
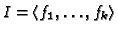
We assume that 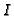 is a radical ideal.
is a radical ideal.
- Output
- Polynomial rings
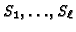 , ideals
, ideals
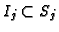 , and maps
, and maps
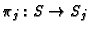 such that
such that
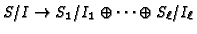 ,
induced by
,
induced by
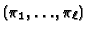 is the normalization map of
is the normalization map of
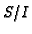 .
.
- Compute an ideal
 describing the singular locus.
describing the singular locus.
- Compute the radical
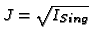 .
.
- Choose
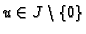 and compute
and compute 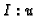 . If
. If
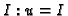 go to 4 (then
go to 4 (then 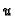 is a non-zerodivisor
of
is a non-zerodivisor
of 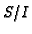 ). Otherwise, set
). Otherwise, set
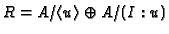 and go to 6.
and go to 6.
- Compute
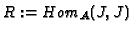 and
and
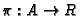 .
.
- If
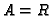 then return
then return 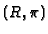 , otherwise go to 1.
, otherwise go to 1.
- Suppose
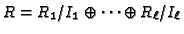 . Then, for each
. Then, for each
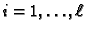 , set
, set
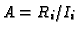 and go to 1.
and go to 1.



Next: Integral closure algorithm
Up: Normalization algorithm
Previous: Computing the non-normal locus
Christoph Lossen
2001-03-21