This algorithm is a generalization of Buchberger's algorithm (which works for wellorderings cf. [B1], [B2]) and Mora's tangent cone algorithm (which works for tangent cone orderings, cf. [M1], [MPT]) and which includes a mixture of both (which is useful for certain applications, in particular to algorithms described by Mora in his Graal paper [M3]). In fact, it is an easy extension of Mora's idea by introducing the ``correct'' definition of ecart. But we present it in a new way which, as we hope, makes the relation to the existing standard basis algorithms transparent.
Let K be a field,
![]() and
and
![]() column vectors in
column vectors in
![]() ,
,
![]() .
Let < be a semigroup
ordering on the set of monomials
.
Let < be a semigroup
ordering on the set of monomials
![]() of K[x],
that is, < is a total ordering and
of K[x],
that is, < is a total ordering and
![]() implies
implies
![]() for any
for any
![]() .
Robbiano (cf. [R]) proved that any semigroup ordering can be defined by a matrix
.
Robbiano (cf. [R]) proved that any semigroup ordering can be defined by a matrix
![]() as follows:
as follows:
Let
![]() be the rows of A, then
be the rows of A, then
![]() if and only if there is an i with
if and only if there is an i with
![]() for j < i and
for j < i and
![]() .
Thus,
.
Thus,
![]() if and only if
if and only if ![]() is smaller than
is smaller than ![]() with
respect to the lexicographical ordering of vectors in
with
respect to the lexicographical ordering of vectors in
![]() .
.
For
![]() ,
,
![]() ,
let
,
let ![]() be the leading monomial
with respect to the ordering < and
be the leading monomial
with respect to the ordering < and ![]() the coefficient of
L(g) in g, that is
g = c(g)L(g) + smaller terms with respect to
<.
the coefficient of
L(g) in g, that is
g = c(g)L(g) + smaller terms with respect to
<.
Important orderings for applications are:
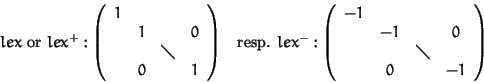

If wi = 1 (respectively wi = -1) for all i we obtain the degree reverse lexicographical ordering, degrevlex+ (respectively degrevlex-).
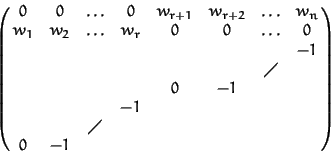
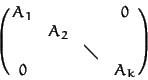
We call an ordering a degree ordering if it is given by a matrix with coefficients of the first row either all positive or all negative. In the positive (respectively negative) case Loc ;SPMlt;K[x] = K[x] (respectively Loc ;SPMlt; K[x] = K[x](x)).
We consider also module orderings <m on the set of ``monomials''
![]() of
of
![]() which are
compatible with the ordering < on K[x]. That is for all monomials
which are
compatible with the ordering < on K[x]. That is for all monomials
![]() and
and
![]() we have: f <m f' implies
pf <m pf' and
p < q implies pf <m qf.
we have: f <m f' implies
pf <m pf' and
p < q implies pf <m qf.
We now fix an ordering <m on K[x]r compatible with < and denote it
also with <. Again we have the notion of coefficient c(f) and leading
monomial L(f). < has the important property:
Note that a reduced standard basis of polynomials does not necessarily exist (cf. Remark 1.12).
The proof will be deduced from the normal form used in the standard basis
algorithm (cf. Corollary 1.11). Note that, in general, it is not true that
![]() generate I as K[x]-module (take
generate I as K[x]-module (take
![]() with lex-).
with lex-).
This is also not true if
![]() is
is
![]() -primary
and if
-primary
and if
![]() is a reduced standard basis:
Consider the ideal
is a reduced standard basis:
Consider the ideal
![]() generated by
generated by
![]() which is (x,y)-primary. The first two elements are a
reduced standard basis of
which is (x,y)-primary. The first two elements are a
reduced standard basis of
![]() where < is
degrevlex- und hence generate
where < is
degrevlex- und hence generate
![]() but they do not generate
but they do not generate
![]() .
(This answers a question of T. Mora.)
.
(This answers a question of T. Mora.)
Notations:
Let
![]() ,
,
![]() and
and
![]() .
If i
= j and
.
If i
= j and
![]() then we write
L(f) | L(g).
then we write
L(f) | L(g).
If i = j and
![]() then
then
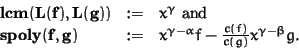
Let
![]() finite and
ordered
finite and
ordered ![]() .
.
The principle for many standard basis algorithms depending on a chosen normal form is the following:
In this language Buchberger's algorithm is just
If < is any ordering (not necessarily a wellordering) and A the
corresponding matrix, then the matrix
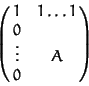
This ordering has the following property:
The Lazard method (cf. [L]) to compute a standard basis is the following:
Mora found for tangent cone orderings (cf. [M1], [MPT]) an algorithm which computes a standard basis over Loc;SPMlt; K[x]. This algorithm can be generalized to any ordering and we can describe it as follows:
Let
![]() be a finite set of homogeneous elements and
be a finite set of homogeneous elements and
![]() homogeneous. Note that an element of K[t, x]r is homogeneous
if its components are homogeneous polynomials of the same degree. The
generalization of Mora's normal form to any semigroup ordering is as follows:
homogeneous. Note that an element of K[t, x]r is homogeneous
if its components are homogeneous polynomials of the same degree. The
generalization of Mora's normal form to any semigroup ordering is as follows:
Proof: 2) By induction suppose that after the ![]() -th step in NFMora we have
-th step in NFMora we have
If
![]() for all
for all ![]() then we have finished.
then we have finished.
Since T consists of elements ![]() and of
and of ![]() constructed in
previous steps we have to consider two cases:
constructed in
previous steps we have to consider two cases:
We obtain
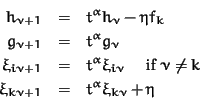
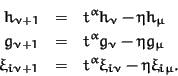
Now
![]() implies
implies
![]() ,
that is
,
that is
![]() .
.
This proves 2).
To prove 1) let
![]() be the set T
after the
be the set T
after the ![]() -th reduction. Let N be an integer such that
-th reduction. Let N be an integer such that
![]() (such N exists because K[t, x]r is noetherian). This implies
(such N exists because K[t, x]r is noetherian). This implies
![]() .
The algorithm
continues with fixed T and terminates because < is a wellordering on K[t,
x]r.
.
The algorithm
continues with fixed T and terminates because < is a wellordering on K[t,
x]r.
The corollary is an easy consequence of 1.9.

Gräbe discovered (cf. [G]) that for a suitable choice of the weights adapted to the input (the polynomials should become as homogeneous as possible with respect to these weights) the algorithm can become faster. We call this the (weighted) ecartMethod.
If we try the same for an arbitrary semigroup ordering, this procedure will,
in general, not terminate. We can only derive a presentation ![]() with
with
![]() and
and
![]() (formal power series) having the above
properties.
(formal power series) having the above
properties.