


Next: 4.6 Saturation
Up: 4. Syzygies
Previous: 4.4 Module intersection 2
Lemma 4..8
The quotient (
I:
J) of two ideals
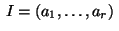
and
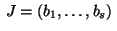
in
R is the kernel of the map
It can be computed as
SINGULAR example (see example in section 2.3.1):
ring R=...;
ideal I=...;
ideal J=...;
quotient(I,J)
| ZCA Home |
Reports |