


Next: 3. Solving the Submodule
Up: Introducing Reduction to Polycyclic
Previous: 1. Introduction
2. Basic Definitions
Let 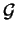 be a group with binary operation
be a group with binary operation  and identity
and identity 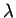 .
The elements of a group ring
.
The elements of a group ring
![${\bf K}[{\cal G}]$](img5.gif) over a field
over a field  can be presented as polynomials
can be presented as polynomials
 where only finitely many coefficients are non-zero.
Addition and multiplication
for two polynomials
where only finitely many coefficients are non-zero.
Addition and multiplication
for two polynomials
 and
and
 are defined as
are defined as
 and
and
 with
with
 .
Polynomials will be written as finite sums
.
Polynomials will be written as finite sums
 with
with
 and
and
 .
.
For a subset F of
![${\bf K}[{\cal G}]$](img5.gif) we can specify special
subsets of
we can specify special
subsets of
![${\bf K}[{\cal G}]$](img5.gif) as follows:
We call the set
as follows:
We call the set
 the right ideal3,
the right ideal3,
 the left ideal, and
the left ideal, and
 the two-sided ideal generated by F.
the two-sided ideal generated by F.
As we are interested in constructing Gröbner bases for ideals in
![${\bf K}[{\cal G}]$](img5.gif) ,
we need an appropriate
presentation of the group
,
we need an appropriate
presentation of the group  in order to do computations.
Structures which can be used to present
groups are semi-Thue systems (also called
string-rewriting systems).
Let us start with some basic definitions.
For a finite alphabet
in order to do computations.
Structures which can be used to present
groups are semi-Thue systems (also called
string-rewriting systems).
Let us start with some basic definitions.
For a finite alphabet  ,
,
 will denote the set of all words over the
alphabet
will denote the set of all words over the
alphabet  where
where  presents the
empty word, i.e.,
the word of length zero.
presents the
empty word, i.e.,
the word of length zero.
 will denote the identity on
will denote the identity on  .
A semi-Thue system
T over
.
A semi-Thue system
T over  is a subset of
is a subset of
 .
The elements (l,r) of T are called
rules and will often be
written as
.
The elements (l,r) of T are called
rules and will often be
written as
 .
The single-step reduction relation
on
.
The single-step reduction relation
on  induced
by a semi-Thue system T is defined as follows:
For any u,v in
induced
by a semi-Thue system T is defined as follows:
For any u,v in  ,
,
 if and only if there exist
x,y in
if and only if there exist
x,y in  and (l,r) in T such that
and (l,r) in T such that
 and
and
 .
The reduction relation
on
.
The reduction relation
on  induced by T is the
reflexive transitive closure of
induced by T is the
reflexive transitive closure of
 and is denoted by
and is denoted by
 .
The reflexive transitive symmetric closure is
denoted by
.
The reflexive transitive symmetric closure is
denoted by
 .
If
.
If
 holds then one says that u reduces to v.
In case u has no descendant except itself it is called irreducible.
The reduction is called Noetherian if and only if there is no
infinite chain
holds then one says that u reduces to v.
In case u has no descendant except itself it is called irreducible.
The reduction is called Noetherian if and only if there is no
infinite chain
 .
We speak of confluence if for all u,v,w in
.
We speak of confluence if for all u,v,w in  ,
,
 and
and
 imply the existence of z in
imply the existence of z in  such that
such that
 and
and
 .
A semi-Thue system is called convergent if it is both, Noetherian
and confluent, i.e., unique normal forms exist for the irreducible elements.
.
A semi-Thue system is called convergent if it is both, Noetherian
and confluent, i.e., unique normal forms exist for the irreducible elements.
Definition 1
Let

be an alphabet.
A mapping

is called an
involution
if

for all
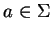
.
A semi-Thue system is called a
group system
if there exists an
involution

such that for all
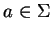
the rules

and

are
included in
T.
Note that sometimes we will assume that
 where
where
 contains the formal inverses
of
contains the formal inverses
of  and T contains the rules corresponding to the
trivial relations in a group, namely
and T contains the rules corresponding to the
trivial relations in a group, namely
 .
.
An equivalence relation on  is said to be a congruence
relation in case it is admissible, i.e., compatible with
concatenation.
Since this is obviously true for the reduction relation induced by a
semi-Thue system T, the reflexive transitive symmetric closure
is said to be a congruence
relation in case it is admissible, i.e., compatible with
concatenation.
Since this is obviously true for the reduction relation induced by a
semi-Thue system T, the reflexive transitive symmetric closure
 is a congruence relation on the set
is a congruence relation on the set  ,
the Thue
congruence .
The congruence classes are denoted by
,
the Thue
congruence .
The congruence classes are denoted by
![$[w]_T = \{ v \in \Sigma^* \mid v
\mbox{$\,\stackrel{*}{\longleftrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } w \}$](img49.gif) and we can set
and we can set
![${\bf M}_T = \{ [w]_T \mid w \in
\Sigma^* \}$](img50.gif) .
In fact
.
In fact  is the factor monoid of the free monoid
is the factor monoid of the free monoid
 modulo the congruence induced by T as the following lemma
establishes.
modulo the congruence induced by T as the following lemma
establishes.
Lemma 1
Let
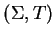 be a semi-Thue system.
be a semi-Thue system.
- 1.
- The set
 together with the binary operation
together with the binary operation
 defined by
defined by
![$[u]_T
\circ [v]_T = [uv]_T$](img54.gif) and the identity
and the identity
![$[\lambda]_T$](img55.gif) is a monoid, called the
factor monoid of
is a monoid, called the
factor monoid of  and
and
 .
.
- 2.
- In case T is a group system, the set
 together with
together with
 ,
,
![$[\lambda]_T$](img55.gif) and
and  is a group, where
is a group, where
![${\sf inv}\/([w]_T) = [{\rm inv}(w)]_T$](img57.gif) ,
and
,
and
 ,
,
 for all
for all
 ,
,
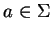 .
.
Hence, semi-Thue systems are means for presenting monoids and groups.
The following definitions are closely related to describing monoids
and groups in terms of generators and defining relations.
We call a pair
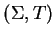 a
presentation of a monoid (group)
a
presentation of a monoid (group)  if
if
 .
Note that every monoid can be presented by a (even convergent)
semi-Thue system.
Just let
.
Note that every monoid can be presented by a (even convergent)
semi-Thue system.
Just let  be the (possibly infinite) set of all elements and T the
multiplication table.
The problem is that this presentation in general is neither finite nor recursive.
We call a monoid (group)
be the (possibly infinite) set of all elements and T the
multiplication table.
The problem is that this presentation in general is neither finite nor recursive.
We call a monoid (group)  finitely generated, if
finitely generated, if  has a
presentation
has a
presentation
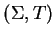 such that
such that  is finite.
is finite.
 is said to be finitely
presented,
if additionally
T is finite.
In order to do effective computations in our monoid or group
we have to be able
to compute representatives for the congruence classes of the elements.
A very nice solution occurs in case we are able to give convergent finite
semi-Thue systems as presentations, since then every congruence
class has a unique representative and many problems, e.g. the word
problem, are algorithmically solvable.
The class of polycyclic groups, which include the Abelian and nilpotent
groups, allow convergent presentations4.
The following notations are taken from [Wi89].
is said to be finitely
presented,
if additionally
T is finite.
In order to do effective computations in our monoid or group
we have to be able
to compute representatives for the congruence classes of the elements.
A very nice solution occurs in case we are able to give convergent finite
semi-Thue systems as presentations, since then every congruence
class has a unique representative and many problems, e.g. the word
problem, are algorithmically solvable.
The class of polycyclic groups, which include the Abelian and nilpotent
groups, allow convergent presentations4.
The following notations are taken from [Wi89].
Let
 be a finite alphabet
and for
be a finite alphabet
and for
 we define the subsets
we define the subsets
 ,
,
 .
We first distinguish several particular classes of rules over
.
We first distinguish several particular classes of rules over  .
.
Definition 3
For

a subset
C of

is called a
commutation system if
- 1.
- C contains only CX-rules, and
- 2.
- for all
 and for all
and for all
 there
is exactly one rule
there
is exactly one rule
 in C.
in C.
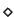
Definition 4
For
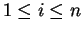
a rule

where

,

is called a
positive P-rule and
a rule

where

and

is called a
negative P-rule.
Then a subset
P of

is called a
power system if
- 1.
- P contains only positive and negative P-rules.
- 2.
- For all
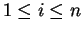 there is a negative P-rule
there is a negative P-rule
 in P if and only if there also
is a positive P-rule of the form
in P if and only if there also
is a positive P-rule of the form
 with
with  in P.
in P.
- 3.
- For all
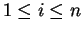 there is at most one negative P-rule
there is at most one negative P-rule
 and at most
one positive P-rule
and at most
one positive P-rule
 in P.
in P.
In combining these rule systems we can characterize special group presentations.
For  in
in
 ,
a presentation
,
a presentation
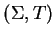 is called a CX-string-rewriting system (CX-system)
if
is called a CX-string-rewriting system (CX-system)
if
 where C is a commutation system and I
contains the trivial rules,
i.e.,
where C is a commutation system and I
contains the trivial rules,
i.e.,
 .
It is called a
PCX-string-rewriting system (PCX-system)
if
.
It is called a
PCX-string-rewriting system (PCX-system)
if
 where T additionally includes a power
system P.
The motivation for such presentations stems from the fact that they can
be used to characterize special classes of groups.
where T additionally includes a power
system P.
The motivation for such presentations stems from the fact that they can
be used to characterize special classes of groups.
Notice that this theorem is a syntactical illustration of the fact that for
finitely generated groups Abelian implies nilpotent which again implies polycyclic.
Using a syllable ordering Wißmann has shown that a PCX-system
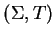 is
a Noetherian string-rewriting system and he gave a completion procedure for such systems
which terminates with an output that is again a PCX-system of the same type.
is
a Noetherian string-rewriting system and he gave a completion procedure for such systems
which terminates with an output that is again a PCX-system of the same type.
Definition 5
Let

be an alphabet and

a partial ordering on

.
We define an ordering

on tuples over

as
follows:
Let
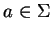
.
Then every

can be uniquely decomposed with respect
to
a as

,
where

and

.
Given a total precedence
2

on

we can define a
syllable ordering with status left by
where
a is the largest letter in

according to

and

,

are the decompositions of
u and
v with respect to
a in case
|
u|
a = |
v|
a =
m.
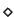
The total precedence used on an alphabet
 in our setting is
in our setting is
 .
Using the syllable ordering induced by this precedence
we can give a characterization of the
elements of our group as
a subset of the set of
ordered group words
.
Using the syllable ordering induced by this precedence
we can give a characterization of the
elements of our group as
a subset of the set of
ordered group words
 ,
where we define
,
where we define
 recursively by
recursively by
 ,
and
,
and
 .
Further with respect to T we define the constants
.
Further with respect to T we define the constants
 for
for
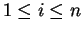 by setting
by setting
One can show that using the syllable ordering for orienting T we get
For example the semi-Thue system
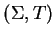 where
where
 such
that we have
such
that we have
 and
and
 is a presentation of the free commutative group generated by
is a presentation of the free commutative group generated by
 and we have
and we have
 .
.
In restricting the syllable ordering introduced in definition
5 to ordered group words this gives us
 if and only if for some
if and only if for some
 we
have il = jl for all
we
have il = jl for all
 and
and
 with
with
 if and only if
if and only if  or
or
 and
and
 or
or
 and
and
 .
where > is the usual ordering5
on
.
where > is the usual ordering5
on  and for
and for
 ,
,
 if
if
 ,
,
 if
if
 and
and
 if
if
 .
We then call ad the distinguishing
letter between the two ordered group words.
.
We then call ad the distinguishing
letter between the two ordered group words.
The next two technical lemmata are related to some properties of the
wellfounded ordering
 and will be useful in the proofs later on.
and will be useful in the proofs later on.
Proof :
1.11.1
In case a > 0 we find  (since
(since
 )
and
)
and  (as
(as
 .
This immediately implies
.
This immediately implies
 and hence
and hence
 .
.
On the other hand, a < 0 gives us  (since
(since
 )
and depending on b either
a + c < b + c < 0 or
)
and depending on b either
a + c < b + c < 0 or
 ,
again implying
,
again implying
 .
.
q.e.d.
1.11
Lemma 3
Let
 .
Then
.
Then
 ,
,
 , and the existence
of an element
, and the existence
of an element
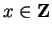 such that
such that
 and
and
 imply
imply
 .
In case
.
In case
 holds we get
holds we get
 .
.
Proof :
1.11.1
First let us look at the case b-a = c-a.
This implies b=c and hence
b+y = c+ y for all
 .
Therefore the existence of an
.
Therefore the existence of an
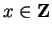 such that
such that
 implies
implies
 .
.
Now it remains to prove that the case
 is not
possible.
is not
possible.
First suppose c-a < 0.
Let us distinguish the two possible cases:
If a>0 we get
 (as
(as
 )
and
)
and
 (as
(as
 ).
Since then
).
Since then
 is not possible,
is not possible,
 implies that we have
c-a < b-a <0
and hence
implies that we have
c-a < b-a <0
and hence
 must hold.
We now show that in this case no x as described in the lemma can be found.
For
must hold.
We now show that in this case no x as described in the lemma can be found.
For
 we get that for all
we get that for all  we have
we have
 and for all y < -b we have
and for all y < -b we have
 .
Similarly, for
.
Similarly, for
 we find that for all
we find that for all  we have
we have
 and for all z<-c,
and for all z<-c,
 holds.
Hence for x such that
holds.
Hence for x such that
 and
and
 to hold,
we must have x<-b and
to hold,
we must have x<-b and  ,
contradicting
,
contradicting
 .
On the other hand, a<0 leads to a contradiction
.
On the other hand, a<0 leads to a contradiction
 as
as
 either implies
either implies  or
or
 .
.
Hence let us suppose c-a > 0 and therefore
 implying
implying
 (and hence
(and hence
 must hold
as
must hold
as  ).
Furthermore,
).
Furthermore,
 implies a < 0.
Let us analyze the remaining cases.
If
implies a < 0.
Let us analyze the remaining cases.
If  we find b < 0 as well (since
we find b < 0 as well (since
 ).
Since the equation
).
Since the equation
 holds for
holds for
 only
and
only
and
 for
for
 only, no
x as required can exist.
Hence suppose c>0.
Then depending on b the equation
only, no
x as required can exist.
Hence suppose c>0.
Then depending on b the equation
 holds
either for
holds
either for
 (in case b < 0) only
or for
(in case b < 0) only
or for
 (in case
(in case  ), and as further
), and as further
 must
hold again no such x can exist.
must
hold again no such x can exist.
q.e.d.
1.11
The following lemma is an easy observation on the results of
multiplying a letter by special ordered group words.
Lemma 4
- 1.
- Let
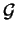 be a nilpotent group with a convergent PCNI-presentation
be a nilpotent group with a convergent PCNI-presentation
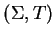 .
Further for some
.
Further for some
 let
let
 ,
,
 .
Then we have
.
Then we have
 and
and
 for some
for some
 .
.
- 2.
- Let
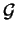 be a polycyclic group with a convergent PCP-presentation
be a polycyclic group with a convergent PCP-presentation
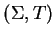 .
Further for some
.
Further for some
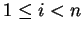 let
let
 .
Then we have
.
Then we have
 for some
for some
 .
.
Proof :
1.11.1
This follows immediately from the rules given in the respective presentations.
q.e.d.
1.11
We now define a new ordering on 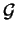 called a tuple ordering, which
will be crucial in our definitions of reduction.
called a tuple ordering, which
will be crucial in our definitions of reduction.
Definition 6
For two elements

,
we define

if for each
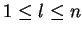
we
have either
jl = 0 or
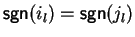
and

where

is the sign of the non-zero integer
i.
Further we define

if

and
|
il|>|
jl|
for some
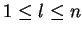
and

for all
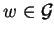
.
According to this ordering we call
v a
syntactic divisor
or
commutative prefix of
w if

.
Notice that this ordering captures the fact that a divisor of a term
in the ordinary polynomial ring is also a commutative prefix of the term.
The tuple ordering is not total on 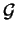 but we find that
but we find that
 implies
implies  ,
where
,
where  is the ordering on
is the ordering on 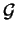 induced
by the syllable ordering used as completion ordering for the respective
PCX-presentation of
induced
by the syllable ordering used as completion ordering for the respective
PCX-presentation of 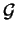 .
Given a non-zero polynomial p in
.
Given a non-zero polynomial p in
![${\bf K}[{\cal G}]$](img5.gif) ,
the so called head term
,
the so called head term
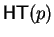 is the largest term in p with respect to
is the largest term in p with respect to  ,
,
 is the
coefficient of this term and the head monomial is
is the
coefficient of this term and the head monomial is
 .
.
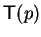 is the set of terms occurring in
p.
The total ordering
is the set of terms occurring in
p.
The total ordering  on
on 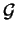 can be extended to a partial ordering on
can be extended to a partial ordering on
![${\bf K}[{\cal G}]$](img5.gif) by setting p > q if and only if
by setting p > q if and only if
 or
or
 and
and
 .
.
The tuple ordering can be used to specify special representations of
right and left ideal elements and special bases of them.
Definition 7
Let
F be a set of polynomials and
p a non-zero
polynomial in
![${\bf K}[{\cal G}]$](img5.gif)
.
- 1.
- A representation
is called a right commutative prefix standard
representation
in case for the respective head terms we have
 and
and
 for all
for all
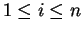 .
In our previous work this was also called a
quasi-commutative (qc-) standard representation.
.
In our previous work this was also called a
quasi-commutative (qc-) standard representation.
- 2.
- A representation
is called a left commutative prefix standard
representation
in case for the respective head terms we have
 and
and
 for all
for all
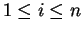 .
Again for historical reasons this is sometimes called a
left polycyclic (lpc-) standard representation.
.
Again for historical reasons this is sometimes called a
left polycyclic (lpc-) standard representation.
A set
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is called a right commutative prefix respectively left commutative prefix
standard basis
if every non-zero polynomial in

respectively
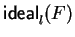
has a right commutative prefix respectively left commutative prefix standard representation with
respect to
F.
Notice that in case 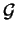 is Abelian these representations coincide and
are called commutative standard representations.
We will later on see how such representations are related to
different reductions, which will be Noetherian
because of the following statements, which heavily depend on the presentation of
the group.
is Abelian these representations coincide and
are called commutative standard representations.
We will later on see how such representations are related to
different reductions, which will be Noetherian
because of the following statements, which heavily depend on the presentation of
the group.
Lemma 5
Let 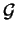 be a nilpotent group with a convergent PCNI-presentation,
be a nilpotent group with a convergent PCNI-presentation,
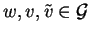 with
with
 and
and
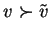 .
Then for
.
Then for
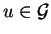 such that
such that
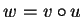 , we get
, we get
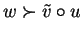 .
Notice that since
.
Notice that since 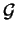 is a group, u always exists and is unique,
namely
is a group, u always exists and is unique,
namely
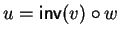 .
.
Proof :
1.11.1
Let ad be the distinguishing letter between v and
 ,
i.e.,
,
i.e.,
 ,
,
 with
with
 ,
,
 and
and
 .
Then for
.
Then for
 we get
we get
 and similarly
and similarly
 and since
and since
 ,
,
 and the exponents of the letter
ad are different, in order to decide whether
and the exponents of the letter
ad are different, in order to decide whether
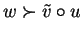 we only have
to compare the exponents of ad in the normal forms of the respective products.
Now,
we only have
to compare the exponents of ad in the normal forms of the respective products.
Now,
 gives us, for the exponent wd of the letter ad in w,
gives us, for the exponent wd of the letter ad in w,
 ,
,
 and
ud + vd + sd = wd or
and
ud + vd + sd = wd or
 in case ad is
bounded by md.
in case ad is
bounded by md.
To show that
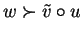 we now have to distinguish two cases.
If the letter ad has unbounded exponents, we can apply lemma 2 since
we now have to distinguish two cases.
If the letter ad has unbounded exponents, we can apply lemma 2 since
 and
and
 hold (the latter follows as
hold (the latter follows as
 ).
Hence let us assume the letter ad is bounded, i.e.,
we know
).
Hence let us assume the letter ad is bounded, i.e.,
we know
 ,
and
since
,
and
since
 must also hold we get
must also hold we get
 and
and
 .
Now in case
vd + ud + sd = wd we are done, as then
.
Now in case
vd + ud + sd = wd we are done, as then
 implies
implies
 .
Else, as
.
Else, as
 ,
for
y = wd - vd we know
,
for
y = wd - vd we know
 with
with
 and hence
and hence
 and we are done.
and we are done.
q.e.d.
1.11
However, the next example shows that for PCP-presentations of groups this
in general no longer holds.
Example 1
Let
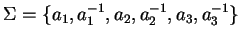
and

be a polycyclic presentation of the free nilpotent group with two generators.
Then for

,

and

we have

,
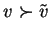
.
Now for

we find

,
but

and hence

.
This example stresses the importance of the presentation chosen for the group, as the group
is nilpotent.
Note that lemma 5 holds when using the presentation
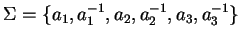 and
and
 .
Then for
.
Then for
 ,
,
 and
and
 we get
we get
 and
and
 .
.
Still for groups with convergent PCP-presentations a similar stability property holds for left multiples.
Lemma 6
Let 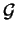 be a polycyclic group with a convergent PCP-presentation,
be a polycyclic group with a convergent PCP-presentation,
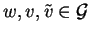 with
with
 and
and
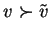 .
Then for
.
Then for
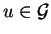 such that
such that
 , we get
, we get
 .
Notice that since
.
Notice that since 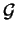 is a group, u always exists and is unique,
namely
is a group, u always exists and is unique,
namely
 .
.
Proof :
1.11.1
Let ad be the distinguishing letter between v and
 ,
i.e.,
,
i.e.,
 ,
,
 with
with
 ,
,
 and
and
 .
Then for
.
Then for
 we get
we get
 with
with
 ,
,
 and similarly
and similarly
 with
with
 .
Furthermore,
.
Furthermore,
 gives us, for the exponent wd of the letter ad in w,
gives us, for the exponent wd of the letter ad in w,
 ,
,
 and
ud + vd + z2 = wd or
and
ud + vd + z2 = wd or
 in case ad is
bounded by md.
To show that
in case ad is
bounded by md.
To show that
 we can proceed as in lemma 5.
we can proceed as in lemma 5.
q.e.d.
1.11
Let us close this section by summarizing Sims' notions for presenting polycyclic
groups as given in chapter 9 of [Si94].
Let
be a polycyclic series for 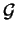 .
For
.
For
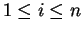 let ai be an element of
let ai be an element of
 whose image in
whose image in
 generates that group.
The letters
generates that group.
The letters
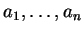 are called a polycyclic generating sequence
and we have
are called a polycyclic generating sequence
and we have
 ,
i.e.,
,
i.e.,
 is the
subgroup of
is the
subgroup of 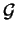 generated by
generated by
 .
Further let
.
Further let
 and for
and for
 set
set
 .
It is assumed that the generating sequence is not redundant in the sense that no
ai is in
.
It is assumed that the generating sequence is not redundant in the sense that no
ai is in
 .
Every element of
.
Every element of 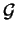 can be expressed in the form
can be expressed in the form
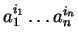 ,
where
,
where
 ,
and such a presentation is called a collected word,
if
,
and such a presentation is called a collected word,
if
 for
for  .
Now
.
Now 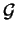 gives rise to a unique presentation called the
standard polycyclic presentation with respect to the letters
gives rise to a unique presentation called the
standard polycyclic presentation with respect to the letters
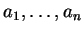 ,
namely
,
namely
| ajai |
= |
 , , |
j>i, |
|
aj-1ai |
= |
 , , |
j>i,
 , , |
|
ajai-1 |
= |
 , , |
j>i,
 , , |
|
ajai-1 |
= |
 , , |
j>i,
 , , |
| aimi |
= |
 |
 , , |
| ai-1 |
= |
 |
 , , |
|
aiai-1 |
= |
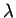 , , |
 , , |
|
ai-1ai |
= |
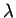 , , |
 , , |
where the right sides are collected words.
Every presentation which has this form defines a polycyclic group, but
there might be ai such that
 although there
is no relation of the form
although there
is no relation of the form
 or only a relation of
the form
or only a relation of
the form
 with n > m.
If this is not true, the presentation is called consistent,
which then is a synonym for confluent.
with n > m.
If this is not true, the presentation is called consistent,
which then is a synonym for confluent.
The relations of such a presentation
can be interpreted as rewriting rules over the alphabet
 with respect to the syllable ordering - here
called wreath ordering - induced by the precedence
with respect to the syllable ordering - here
called wreath ordering - induced by the precedence
 .
Then a consistent polycyclic presentation gives rise to a convergent PCP presentation.
.
Then a consistent polycyclic presentation gives rise to a convergent PCP presentation.



Next: 3. Solving the Submodule
Up: Introducing Reduction to Polycyclic
Previous: 1. Introduction
| ZCA Home |
Reports |
![]() we can specify special
subsets of
we can specify special
subsets of
![]() as follows:
We call the set
as follows:
We call the set
![]() the right ideal3,
the right ideal3,
![]() the left ideal, and
the left ideal, and
![]() the two-sided ideal generated by F.
the two-sided ideal generated by F.
![]() ,
we need an appropriate
presentation of the group
,
we need an appropriate
presentation of the group ![]() in order to do computations.
Structures which can be used to present
groups are semi-Thue systems (also called
string-rewriting systems).
Let us start with some basic definitions.
For a finite alphabet
in order to do computations.
Structures which can be used to present
groups are semi-Thue systems (also called
string-rewriting systems).
Let us start with some basic definitions.
For a finite alphabet ![]() ,
,
![]() will denote the set of all words over the
alphabet
will denote the set of all words over the
alphabet ![]() where
where ![]() presents the
empty word, i.e.,
the word of length zero.
presents the
empty word, i.e.,
the word of length zero.
![]() will denote the identity on
will denote the identity on ![]() .
A semi-Thue system
T over
.
A semi-Thue system
T over ![]() is a subset of
is a subset of
![]() .
The elements (l,r) of T are called
rules and will often be
written as
.
The elements (l,r) of T are called
rules and will often be
written as
![]() .
The single-step reduction relation
on
.
The single-step reduction relation
on ![]() induced
by a semi-Thue system T is defined as follows:
For any u,v in
induced
by a semi-Thue system T is defined as follows:
For any u,v in ![]() ,
,
![]() if and only if there exist
x,y in
if and only if there exist
x,y in ![]() and (l,r) in T such that
and (l,r) in T such that
![]() and
and
![]() .
The reduction relation
on
.
The reduction relation
on ![]() induced by T is the
reflexive transitive closure of
induced by T is the
reflexive transitive closure of
![]() and is denoted by
and is denoted by
![]() .
The reflexive transitive symmetric closure is
denoted by
.
The reflexive transitive symmetric closure is
denoted by
![]() .
If
.
If
![]() holds then one says that u reduces to v.
In case u has no descendant except itself it is called irreducible.
The reduction is called Noetherian if and only if there is no
infinite chain
holds then one says that u reduces to v.
In case u has no descendant except itself it is called irreducible.
The reduction is called Noetherian if and only if there is no
infinite chain
![]() .
We speak of confluence if for all u,v,w in
.
We speak of confluence if for all u,v,w in ![]() ,
,
![]() and
and
![]() imply the existence of z in
imply the existence of z in ![]() such that
such that
![]() and
and
![]() .
A semi-Thue system is called convergent if it is both, Noetherian
and confluent, i.e., unique normal forms exist for the irreducible elements.
.
A semi-Thue system is called convergent if it is both, Noetherian
and confluent, i.e., unique normal forms exist for the irreducible elements. ![]() is said to be a congruence
relation in case it is admissible, i.e., compatible with
concatenation.
Since this is obviously true for the reduction relation induced by a
semi-Thue system T, the reflexive transitive symmetric closure
is said to be a congruence
relation in case it is admissible, i.e., compatible with
concatenation.
Since this is obviously true for the reduction relation induced by a
semi-Thue system T, the reflexive transitive symmetric closure
![]() is a congruence relation on the set
is a congruence relation on the set ![]() ,
the Thue
congruence .
The congruence classes are denoted by
,
the Thue
congruence .
The congruence classes are denoted by
![]() and we can set
and we can set
![]() .
In fact
.
In fact ![]() is the factor monoid of the free monoid
is the factor monoid of the free monoid
![]() modulo the congruence induced by T as the following lemma
establishes.
modulo the congruence induced by T as the following lemma
establishes. ![]() be a finite alphabet
and for
be a finite alphabet
and for
![]() we define the subsets
we define the subsets
![]() ,
,
![]() .
We first distinguish several particular classes of rules over
.
We first distinguish several particular classes of rules over ![]() .
.![]() is
a Noetherian string-rewriting system and he gave a completion procedure for such systems
which terminates with an output that is again a PCX-system of the same type.
is
a Noetherian string-rewriting system and he gave a completion procedure for such systems
which terminates with an output that is again a PCX-system of the same type.
![]() if and only if for some
if and only if for some
![]() we
have il = jl for all
we
have il = jl for all
![]() and
and
![]() with
with
![]() if and only if
if and only if ![]() or
or
![]() and
and
![]() or
or
![]() and
and
![]() .
where > is the usual ordering5
on
.
where > is the usual ordering5
on ![]() and for
and for
![]() ,
,
![]() if
if
![]() ,
,
![]() if
if
![]() and
and
![]() if
if
![]() .
We then call ad the distinguishing
letter between the two ordered group words.
.
We then call ad the distinguishing
letter between the two ordered group words.
![]() and will be useful in the proofs later on.
and will be useful in the proofs later on.
![]() called a tuple ordering, which
will be crucial in our definitions of reduction.
called a tuple ordering, which
will be crucial in our definitions of reduction.

![]() we now have to distinguish two cases.
If the letter ad has unbounded exponents, we can apply lemma 2 since
we now have to distinguish two cases.
If the letter ad has unbounded exponents, we can apply lemma 2 since
![]() and
and
![]() hold (the latter follows as
hold (the latter follows as
![]() ).
Hence let us assume the letter ad is bounded, i.e.,
we know
).
Hence let us assume the letter ad is bounded, i.e.,
we know
![]() ,
and
since
,
and
since
![]() must also hold we get
must also hold we get
![]() and
and
![]() .
Now in case
vd + ud + sd = wd we are done, as then
.
Now in case
vd + ud + sd = wd we are done, as then
![]() implies
implies
![]() .
Else, as
.
Else, as
![]() ,
for
y = wd - vd we know
,
for
y = wd - vd we know
![]() with
with
![]() and hence
and hence
![]() and we are done.
and we are done.
![]() although there
is no relation of the form
although there
is no relation of the form
![]() or only a relation of
the form
or only a relation of
the form
![]() with n > m.
If this is not true, the presentation is called consistent,
which then is a synonym for confluent.
with n > m.
If this is not true, the presentation is called consistent,
which then is a synonym for confluent.
![]() with respect to the syllable ordering - here
called wreath ordering - induced by the precedence
with respect to the syllable ordering - here
called wreath ordering - induced by the precedence
![]() .
Then a consistent polycyclic presentation gives rise to a convergent PCP presentation.
.
Then a consistent polycyclic presentation gives rise to a convergent PCP presentation.