... Reinert¹

The author was supported by the Deutsche Forschungsgemeinschaft (DFG).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... precedence²

By a precedence on an alphabet we mean a partial ordering on its letters.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ideal³

Notice that the linear combinations in these definitions of ideals in fact describe elements of ${\bf K}[{\cal G}]$. Since the elements $\alpha_i \in {\bf K}$ and $w_i \in {\cal G}$ can be interpreted as elements of ${\bf K}[{\cal G}]$ the multiplication $f_i \ast w_i$ is well-defined and gives us an element say h_i in ${\bf K}[{\cal G}]$, as does again the multiplcation $\alpha_i \cdot h_i$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... presentations⁴

A survey on groups allowing convergent presentations can be found in [MaOt89].

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ordering⁵

By the usual ordering on ${\bf Z}$ we mean $\ldots -3 < -2 < -1 < 0 < 1 < 2 < 3 < \ldots$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...

I.e. tex2html_wrap_inline$= (+ - 1)/2 $.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... terminate⁶

This can also be seen, since for m we have $a^m \in {\cal H}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

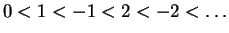...$0 < 1 < -1 < 2 < -2 < \ldots$⁷

E.g. we get $a_1 \prec a_1^{-1} \prec a_1^3a_2 \prec a_1a_2^2 \prec a_1^{-1}a_2^2 \prec a_1a_2^{-2}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... in⁸

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... set⁹

see [Si94] page 503 for the concrete computation.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... basis¹⁰

This set is the union of the qc-saturating sets $\mbox{\sc Sat}_{qc}(a_1a_3a_5 -1) = \{ a_1 - a_3^2a_4^2a_5, a_1^2 -a_3a_4a_5 \}$, $\mbox{\sc Sat}_{qc}(a_2a_3 -1) = \{ a_2-a_3^2a_4^2a_5^2, a_2^2 -a_3a_4a_5 \}$, $\mbox{\sc Sat}_{qc}(a_4a_5^2 -1) = \{ a_4-a_5, a_4^2 -2 \}$, $\mbox{\sc Sat}_{qc}(a_5-1) = \{ a_5-1, a_5^2 -1 \}$ and it is a Gröbner basis as all s-polynomials reduce to zero.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... basis¹¹

While interreduction in group rings can destroy the property of being a Gröbner basis for certain reductions, qc-reduction allows to incorporate this idea into Gröbner basis computations and produces unique monic reduced Gröbner bases.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... bounded¹²

In case a_k is bounded we can still use negative powers of a_k in the computations, as from the point of view of the collection process it does not matter, at what time the power rules for a_k are applied. We only have to take into account that in the definition of w₁ = a_k^{-l_k + i_k} the normal form looks different in case -l_k + i_k < 0.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ring¹³

compare page .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... bounded¹⁴

In case a_k is bounded we can still use negative powers of a_k in the computations, as from the point of view of the collection process it does not matter, at what time the power rules for a_k are applied.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... convergent¹⁵

For a proof of this see section 8.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... none¹⁶

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...

``none'' in this context means that no reduction based on commutative divisors and using right multiples exists.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.