Next: 3. Relating the Word Up: Relating Rewriting Techniques on Previous: 1. Introduction

2. Presentations: Congruences in Monoids and Groups

The book of Lallement [La79] gives a good introduction to congruences and presentations of monoids, while the book of Johnson [Jo76] was used as a source on group presentations.

Let A be a set and $\rho \subseteq A \times A$ a binary relation on A. By $\epsilon$ we denote the special relation $\{ (a,a) \mid a \in A \}$ . A binary relation $\rho$ is called an equivalence relation in case it is reflexive (i.e. $\epsilon \subseteq \rho$ ), symmetric (i.e. $\rho \subseteq \rho^{-1}= \{ (b,a) \mid (a,b) \in \rho \}$ ) and transitive (i.e. $\rho \circ\rho = \{ (a,c) \mid (a,b),(b,c) \in \rho \} \subseteq \rho$ ). In the following we assume that $\rho$ is an equivalence relation. For an element $a \in A$ we call the set $[a]_{\rho} = \{ a' \in A \mid (a,a') \in \rho \}$ the class of a modulo $\rho$ . Then A is a disjoint union of classes modulo $\rho$ and the set of all such classes modulo $\rho$ is called the quotient of A modulo $\rho$ , denoted by $A / \rho$ .

A congruence on a monoid ${\cal M}$ is defined as an equivalence relation $\rho$ on the set ${\cal M}$ which is stable under left and right multiplication with elements of ${\cal M}$ . In particular a right (respectively left) congruence on ${\cal M}$ is stable with respect to right (respectively left) multiplication.

Given a congruence $\rho$ on a monoid ${\cal M}$ and an element $m \in {\cal M}$ , we call $[m]_{\rho} = \{ m' \in {\cal M}\mid (m, m') \in \rho \}$ the congruence class of m. We can define a monoid structure on the set of all congruence classes $M / \rho$ by setting $[m]_{\rho} \circ_{M / \rho} [m']_{\rho} = [m \circ_{{\cal M}} m']_{\rho}$ for $m, m' \in {\cal M}$ . Then $M / \rho$ is called the quotient of ${\cal M}$ by $\rho$ and the homomorphism $\chi_{\rho} : {\cal M}\longrightarrow{\cal M}/ \rho$ induced by $m \longmapsto [m]_{\rho}$ is in fact surjective.

Congruences now provide the means to construct presentations of monoids. A set of symbols $\Sigma$ is called a set of generators for ${\cal M}$ under the mapping $\phi: \Sigma \longrightarrow{\cal M}$ , if the extension of $\phi$ to the set of words $\Sigma^*$ on $\Sigma$ defined by $\phi(a_1 \ldots a_n) = \phi(a_1) \circ_{{\cal M}} \ldots \circ_{{\cal M}} \phi(a_n)$ , is a homomorphism from $\Sigma^*$ onto ${\cal M}$ . If for two words $w,w' \in \Sigma^*$ we have $\phi(w) = \phi(w')$ we say that ${\cal M}$ satisfies the relation w = w'. The word problem for a monoid ${\cal M}$ now is to decide whether for two words $w,w' \in \Sigma^*$ , ${\cal M}$ satisfies the relation w = w'.

Given a set of relations R we say that a word u is directly derivable from an other word v under the relation $(l,r) \in R$ , if either u = xly and v = xry or u = xry and v = xly for words x,y. We call u derivable from v under R if there exist words $v_0, \ldots , v_n$ such that v= v₀, v_i+1 is directly derivable from v_i for $0 \leq i \leq n-1$ and v_n = u. Notice that if u is derivable from v under R, then $\phi(u) = \phi(v)$ holds, i.e. u=v is a relation in ${\cal M}$ . We then call the relation a consequence of the relations R. In case all and only relations on ${\cal M}$ are consequences of the relations R we say that $(\Sigma, R)$ is a presentation of ${\cal M}$ defined by $\phi$ . $(\Sigma, R)$ is also called a Thue system in the literature.

Now the easiest way to give a presentation of a monoid ${\cal M}$ is to take the set ${\cal M}$ itself as a generating set and to use the multiplication table of ${\cal M}$ as the defining relations. However this presentation in general will not be finite and other presentations fulfilling additional conditions, e.g. finitely many generators of finitely many relations, are hoped for.

In order to construct a presentation of a monoid ${\cal M}$ one has to

1.: Find a set of generators $\Sigma$ for ${\cal M}$ . Then $\phi: \Sigma \longrightarrow{\cal M}$ can be chosen as the natural inclusion mapping.
2.: Find a set of relations R in ${\cal M}$ such that the smallest congruence containing these relations coincides with the kernel congruence of the extended homomorphism $\phi : \Sigma^* \longrightarrow{\cal M}$ . This kernel congruence is $\{ (u,v) \in \Sigma^* \times \Sigma^* \mid \phi(u) =_{{\cal M}} \phi(v) \}$ .

In order to use reduction techniques for computations in monoids or groups, presentations are provided with an orientation of the relations and treated as string rewriting systems (for a general reference of the terms and techniques described here see [BoOt93]). For a finite alphabet $\Sigma$ , again $\Sigma^*$ will denote the set of all words over the alphabet $\Sigma$ where $\lambda$ presents the empty word, i.e., the word of length zero. $\equiv$ will denote the identity on $\Sigma^*$ . A string rewriting system or semi-Thue system is a pair $(\Sigma,T)$ where T is a subset of $\Sigma^* \times \Sigma^*$ . The elements (l,r) of T are called rules and will often be written as $l \longrightarrow r$ . The (single-step) reduction relation on $\Sigma^*$ induced by a set of rules T is defined as follows: For any u,v in $\Sigma^*$ , $u \longrightarrow_T v$ if and only if there exist x,y in $\Sigma^*$ and (l,r) in T such that $u \equiv xly$ and $v \equiv xry$ . v is then called a proper descendant of u. The reflexive transitive symmetric closure is denoted by $\mbox{$\,\stackrel{*}{\longleftrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ }$ and is called the Thue congruence. If $u \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } v$ holds then one says that u reduces to v. In case for u there exists no v such that $u \mbox{$\,\stackrel{+}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } v$ holds, i.e. at least one reduction step must take place, u is called irreducible. An irreducible descendant of u is called a (T-)normal form and is sometimes denoted by $u\!\!\downarrow_{T}$ . The reduction relation induced by T is called Noetherian if and only if there is no infinite chain $u \mbox{$\,\stackrel{}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } v_1 \mbox{... ...} v_2 \mbox{$\,\stackrel{}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } \ldots$ . It is called confluent if for all u,v,w in $\Sigma^*$ , $u \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } v$ and $u \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } w$ imply the existence of z in $\Sigma^*$ such that $v \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } z$ and $w \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } z$ . A string rewriting system is called convergent or complete if it is both, Noetherian and confluent, i.e., unique normal forms exist.

By Newman's lemma we know that under the hypothesis that a reduction relation is Noetherian, a string rewriting system is confluent if and only if it is locally confluent, i.e., for all u,v,w in $\Sigma^*$ , $u \mbox{$\,\stackrel{}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } v$ and $u \mbox{$\,\stackrel{}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } w$ imply the existence of z in $\Sigma^*$ such that $v \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } z$ and $w \mbox{$\,\stackrel{*}{\longrightarrow}\!\!\mbox{}^{{\rm }}_{T}\,$ } z$ . For finite string rewriting systems the global property of being locally confluent can be localized to enable a finite confluence test. Remember that presentations of monoids can be treated as string rewriting systems and notice that string rewriting systems are in fact presentations of monoids. Hence, in case they are finite, convergent and effective, we can ``compute'' in the monoid using the irreducible elements as representatives for the monoid elements. The process of trying to turn a Noetherian string rewriting system into a convergent one by resolving the not locally confluent situations is called completion. We will now sketch how a finite string rewriting system $(\Sigma,T)$ presenting a monoid can be completed in case we have a total admissible² well-founded³ ordering $\succeq$ on $\Sigma^*$ such that for all $(l,r) \in T$ we have $l \succ r$ . This ordering then will be called a completion ordering for T and the completion process transforms $(\Sigma,T)$ into a (not necessarily finite) convergent string rewriting system presenting the same monoid. It is important that in order to check a finite Noetherian string rewriting system T for confluence we only have to look at a finite set of critical situations: for two not necessarily different rules (l₁,r₁),(l₂,r₂) in T the set of critical pairs is defined as $\{ \langle xr_1,r_2y \rangle \mid x,y \in \Sigma^*, xl_1 \equiv l_2y, \vert x\... ...angle \mid x,y \in \Sigma^*, l_1 \equiv xl_2y, \vert x\vert<\vert l_1\vert \}$ . Now given a finite string rewriting system $(\Sigma,T)$ with a completion ordering $\succeq$ we can specify a completion process as follows:

Procedure: KNUTH BENDIX COMPLETION

height 0.5pt <

height 0.5pt tex2html_comment_mark>


Given: 		 A string rewriting system 

,
		 and a total well-founded admissible ordering .
[2ex]

;


;
while 


do
		 

;
		    % Remove an element using a fair strategy
		 for all  critical pairs 


do
		 % 


= 		                    


		  % 		   


				 

;
				 

;
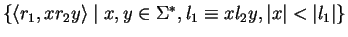
				 % normal.form(z, 


 
Since the word problem for arbitrary string rewriting systems is undecidable, 
 this procedure
 in general will not terminate.
Nevertheless, using a fair⁴
 strategy to remove elements from the set B, it
 always enumerates a convergent string rewriting system based on the completion 
 ordering 
presenting the same
 monoid as the input system.





 

 

   


 Next: 3. Relating the Word
 Up: Relating Rewriting Techniques on
 Previous: 1. Introduction


 |  ZCA Home  | 
 Reports  |