- ... Reinert1
- The author
was supported by the Deutsche Forschungsgemeinschaft (DFG).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... admissible2
- A partial
ordering
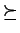 on
on 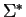 is called admissible if for all u,v,x,y
in
is called admissible if for all u,v,x,y
in 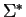 we have
we have
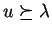 ,
and
,
and
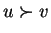 implies
implies
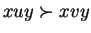 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... well-founded3
- A partial
ordering
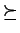 on
on 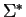 is called well-founded if no infinite
chains of the form
is called well-founded if no infinite
chains of the form
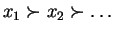 with
with
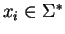 are possible.
are possible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fair4
- A fair strategy will ensure that all
elements of the set B are considered at some time by the procedure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
- These polynomials are frequently called s-polynomials in the literature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
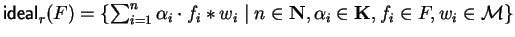 5
5
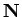 denotes the natural numbers
including 0.
denotes the natural numbers
including 0.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... closure6
- The normal closure of a set T in
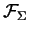 is the smallest
normal subgroup containing T.
is the smallest
normal subgroup containing T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... none7
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
- By theorem
6 the existence of such finite bases would solve the
word problem for groups presented by finite
string rewriting systems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.