


Next: 6. Finding a J-row-reduction
Up: Splitting algorithm for vector
Previous: 4. Splitting criteria
(5.1)
Fix
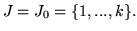 Consider all those matrices
Consider all those matrices
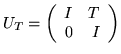 from
from  which do not increase
which do not increase
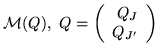 ,
and set
,
and set
Because
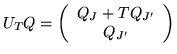 and
and
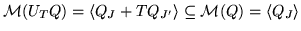 if and only if
if and only if
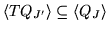 ,
we obtain:
,
we obtain:
Choose a basis
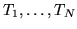 of the module
of the module
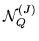 and
a set of associated matrices
and
a set of associated matrices
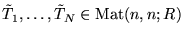 .
.
Proposition 9 ((sufficient condition for
J-row-minimality))
Q is
J-row-minimal if either
(i1)
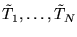 do not have a unit entry; i.e.,
do not have a unit entry; i.e.,
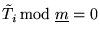
or
(i2) for any
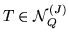 ,
the corresponding
matrix
,
the corresponding
matrix 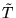 satisfies the condition:
satisfies the condition:
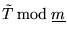 is nilpotent.
is nilpotent.
Condition (i1) implies (i2). Assuming (i2), we obtain for any
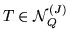
because
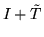 is invertible. Therefore Q is J-row-minimal.
is invertible. Therefore Q is J-row-minimal.
(5.2)
In order to obtain a necessary condition for row-minimality, we have to improve
the choice of a good representative
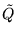 in the equivalence class of Q, cf. (3.3).
Write
in the equivalence class of Q, cf. (3.3).
Write 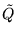 in block form
in block form
We may assume that the columns of A form a completely reduced, minimal
basis of
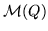 .
This means the columns of A form a minimal system of
generators, increasingly ordered, and the l-th generator is reduced with
respect to the standard basis generated by the first l-1 generators
for appropriate l.
.
This means the columns of A form a minimal system of
generators, increasingly ordered, and the l-th generator is reduced with
respect to the standard basis generated by the first l-1 generators
for appropriate l.
Lemma 10
Let
Q be a submodule of
Rk, given by a completely reduced, minimal
basis
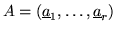
.
A submodule
P of
Q is proper
if and only if
lead(
P),
the initial module, does not contain all leading terms of
A.
We want to show that for a proper submodule P the minimal leading
term not contained in lead(Q) must be in lead(A). Assume the contrary; i.e.
the minimal
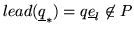 is not contained in lead(A).
We introduce the module
is not contained in lead(A).
We introduce the module
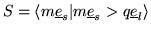 ,
generated by all monomials
in Rk which are greater than
,
generated by all monomials
in Rk which are greater than
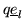 .
.
Considering the whole situation in the factor module Rn/S, we have
the equation
and, from the assumption on reducedness, it follows that all gi
belong to the maximal ideal
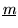 .
The staircases of both modules Q and P are identical up to
.
The staircases of both modules Q and P are identical up to
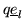 ,
and,
hence, for every generator
,
and,
hence, for every generator
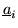 an equation
an equation
with 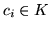 exists. We obtain
exists. We obtain
The second summand vanishes in Rn/S. Thus,
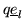 must be a leading term of P,
too.
must be a leading term of P,
too.
The other implication is a well-known fact about standard basis.
(5.3)
Without loss of generality we will assume that
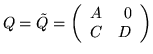 fulfills the conditions of (5.2).
For
fulfills the conditions of (5.2).
For
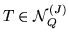 we obtain
we obtain
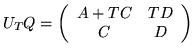 and
and
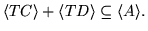 Therefore, matrices
Therefore, matrices
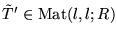



Next: 6. Finding a J-row-reduction
Up: Splitting algorithm for vector
Previous: 4. Splitting criteria
| ZCA Home |
Reports |
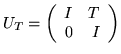 from
from 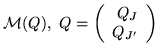 ,
and set
,
and set
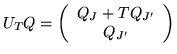 and
and
do not have a unit entry; i.e.,
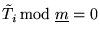
, the corresponding matrix
satisfies the condition:
is nilpotent.
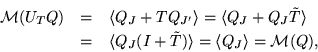
![]() in the equivalence class of Q, cf. (3.3).
Write
in the equivalence class of Q, cf. (3.3).
Write ![]() in block form
in block form
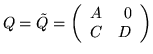 fulfills the conditions of (5.2).
For
fulfills the conditions of (5.2).
For
![]() we obtain
we obtain
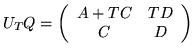 and
and
![]() Therefore, matrices
Therefore, matrices
![]()