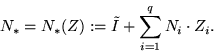
(6.2)
If our presentation matrix Q splits with respect to J,
then by Lemma 2 there exists a unique minimal module
![]() in
in
![]() This fact will reduce (6.1) to a linear problem! Otherwise we could stop and try another subset
J of rows of Q.
This fact will reduce (6.1) to a linear problem! Otherwise we could stop and try another subset
J of rows of Q.
(6.3)
Let
![]() be the set of leading monomials
of the minimal generating system of
be the set of leading monomials
of the minimal generating system of
![]() , formed by the columns of
A, cf. (5.2).
Take the first index
, formed by the columns of
A, cf. (5.2).
Take the first index ![]() such that ms is not a leading term of
such that ms is not a leading term of
![]() .
Let Rk(ms), resp.
Rk+(ms), denote the quotient of Rk
by the submodule of
all monomials greater than or equal to ms, resp. strictly greater than ms, with
respect to the monomial order of Rk.
.
Let Rk(ms), resp.
Rk+(ms), denote the quotient of Rk
by the submodule of
all monomials greater than or equal to ms, resp. strictly greater than ms, with
respect to the monomial order of Rk.
By our choice,
![]() and
and
![]() have the same image in
Rk(ms) and
have the same image in
Rk(ms) and
![]() is still the unique minimal a an
Rk+ (ms)-submodule. It is therefore
of K-codimension 1
with respect to
is still the unique minimal a an
Rk+ (ms)-submodule. It is therefore
of K-codimension 1
with respect to
![]() .
Subsequentely, any strict reduction
.
Subsequentely, any strict reduction
![]() of
of
![]() in
Rk+(ms)
will induce
in
Rk+(ms)
will induce
![]() in
Rk+(ms).
in
Rk+(ms).
(6.4)
By construction we have
![]() for j>s in R+(ms); hence,
for j>s in R+(ms); hence,
![]() is determined by the submatrix NT(s) of the first s
columns of NT.
is determined by the submatrix NT(s) of the first s
columns of NT.
(i1),
(i2).
(i3)splits with respect to J, then the linear space spanned by the columns of
:
is either Ks or a fixed hyperplane
in case
is a zero of the ideal minor(s).
(6.5)
If Q is J-split, the set of zeros of the ideal minor(s) form
a linear subspace with respect to Z:
Note that the radical of an ideal may be computed by just taking annihilators of certain Ext-groups (cf. [EV]). This method is implemented as a procedure in SINGULAR, using only syzygy- and standard-basis-computations. Hence finding a J-row-reduction reduces to solving linear equations if there exists a unique minimal.
Let
![]() and
and
![]() be a zero
of minor(s). Then
be a zero
of minor(s). Then
![]() ,
and consequently
Then regular constant matrices
,
and consequently
Then regular constant matrices
![]() ,
,
![]() exist such that
exist such that
(6.6)
Note that the minor ideal need not to be reduced, as demonstrated by
the following example:
Given
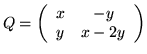 ,
then a representative in the sense of (5.2) is given by
,
then a representative in the sense of (5.2) is given by
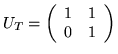 ,
T=(1).
Then
,
T=(1).
Then
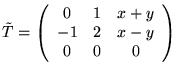 ,
,
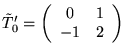 and
and
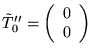 .
Thus
.
Thus
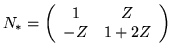 ,
and
minor(N*) = (1+2Z+Z2) = (1+Z)2 is not reduced.
,
and
minor(N*) = (1+2Z+Z2) = (1+Z)2 is not reduced.