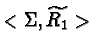 .
This is done in this section by choosing relators from
.
This is done in this section by choosing relators from 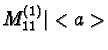 ,
,
In Section 2 we explained, that instead of studying the
index of the subgroup generated by ![]() in
in ![]() for
for
![]() we can instead study the index of the subgroup generated
by
we can instead study the index of the subgroup generated
by ![]() in
in ![]() where
where ![]() is the group
generated by
is the group
generated by ![]() , respectively
, respectively
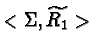 .
This is done in this section by choosing relators from
.
This is done in this section by choosing relators from ![]() , i.e. splitting
, i.e. splitting
![]() , and then trying to complete
, and then trying to complete ![]() with respect to the
ordering chosen using the Knuth-Bendix completion procedure.
When this can be done successfully, Gröbner basis techniques in more general
group rings can be applied.
For example, provided the relators are of the form
with respect to the
ordering chosen using the Knuth-Bendix completion procedure.
When this can be done successfully, Gröbner basis techniques in more general
group rings can be applied.
For example, provided the relators are of the form ![]() ,
where
,
where
![]() and
and
![]() , we can use the Knuth-Bendix
completion procedure to get a finite,
convergent presentation of the underlying group.
For the examples
, we can use the Knuth-Bendix
completion procedure to get a finite,
convergent presentation of the underlying group.
For the examples ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
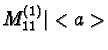 ,
,
![]() ,
,
![]() and
and
![]() all relators having this form were used to
define the new respective groups
all relators having this form were used to
define the new respective groups ![]() (see Table 2).
(see Table 2).
The example ![]() in general gives better results than before,
that is, fewer cosets are enumerated.
The best result is now 45/45 cosets enumerated maximal/total for syl-l-abAB
and I-ALL compared to 143/143 for kbo-A and NONE.
in general gives better results than before,
that is, fewer cosets are enumerated.
The best result is now 45/45 cosets enumerated maximal/total for syl-l-abAB
and I-ALL compared to 143/143 for kbo-A and NONE.
For
![]() on the other hand we get worse results, that is
for most combinations more cosets have to be enumerated.
The best result now is 913/1045 cosets enumerated maximal/total for syl-l-CcBbAa
and P-R compared to 821/867 for kbo-a and P-ALL.
on the other hand we get worse results, that is
for most combinations more cosets have to be enumerated.
The best result now is 913/1045 cosets enumerated maximal/total for syl-l-CcBbAa
and P-R compared to 821/867 for kbo-a and P-ALL.
For ![]() we get optimal results for all orderings combined with
strategy NONE.
All other combinations are equally good or better, with two exceptions, namely
strategy I-R combined with the syllable ordrings.
we get optimal results for all orderings combined with
strategy NONE.
All other combinations are equally good or better, with two exceptions, namely
strategy I-R combined with the syllable ordrings.
For ![]() we get better results for most combinations but the are
quite some combinations which behave worse.
The best result improved to 1092/1103 cosets enumerated maximal/total for
kbo-B and NONE compared to 1105/1566 for kbo-A and P-R.
we get better results for most combinations but the are
quite some combinations which behave worse.
The best result improved to 1092/1103 cosets enumerated maximal/total for
kbo-B and NONE compared to 1105/1566 for kbo-A and P-R.
For
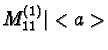 most combinations are worse and only a few are
better.
The best result which was already optimal remained the same.
most combinations are worse and only a few are
better.
The best result which was already optimal remained the same.
For
![]() we have almost as many combinations which
are better as those which are worse.
The best result improved to 448/549 cosets enumerated maximal/total for
syl-l-abAB and I-R compared to 766/773 for kbo-A and NONE.
we have almost as many combinations which
are better as those which are worse.
The best result improved to 448/549 cosets enumerated maximal/total for
syl-l-abAB and I-R compared to 766/773 for kbo-A and NONE.
For ![]() holds the same.
The best result improved to 560/656 cosets enumerated maximal/total for
syl-l-CcBbAa and NONE compared to 1637/1671 for ll-CcBbAa and I-R.
holds the same.
The best result improved to 560/656 cosets enumerated maximal/total for
syl-l-CcBbAa and NONE compared to 1637/1671 for ll-CcBbAa and I-R.
For
![]() again we have a mix of better and worse combinations.
The best result improved to 30949/42538 cosets enumerated maximal/total for
ll-abcABC and P-ALL compared to 43931/56621 for syl-l-CcBbAa and P-ALL.
But it is still worse than the best results for Felsch.
Nevertheless, we are about as good as the default strategy of Felsch type.
again we have a mix of better and worse combinations.
The best result improved to 30949/42538 cosets enumerated maximal/total for
ll-abcABC and P-ALL compared to 43931/56621 for syl-l-CcBbAa and P-ALL.
But it is still worse than the best results for Felsch.
Nevertheless, we are about as good as the default strategy of Felsch type.
Overall, we have the same problem as before.
We have no hints about which combination to choose to get good results for
the coset enumeration process.
Nevertheless, we have an additional parameter to further improve this process.
It should be noted, that we also have the choice not to add all of the relators
having the form ![]() .
That is, we can move only some of them or even other relators, provided that there
exists a finite and convergent presentation of the underlying group.
.
That is, we can move only some of them or even other relators, provided that there
exists a finite and convergent presentation of the underlying group.
For example, in Appendix E.3
the results for the example
![]() are tabulated but this time
we split the set of relators
are tabulated but this time
we split the set of relators ![]() into
into
![]() and
and
![]() .
This was inspired by the fact that
.
This was inspired by the fact that ![]() is one of the generators of the
subgroup.
As before some combinations yielded better results some worse.
The best result was 911/995 cosets enumerated maximal/total for
kbo-C and P-ALL and lies between the best result for the standard
enumeration, which was 821/867 for kbo-a and P-ALL, and the best result for
the first modified enumeration, which is 913/1045 for syl-l-CcBbAa and P-R.
is one of the generators of the
subgroup.
As before some combinations yielded better results some worse.
The best result was 911/995 cosets enumerated maximal/total for
kbo-C and P-ALL and lies between the best result for the standard
enumeration, which was 821/867 for kbo-a and P-ALL, and the best result for
the first modified enumeration, which is 913/1045 for syl-l-CcBbAa and P-R.