- ... matrices1
- These matrices can be computed during the
Gröbner basis computation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... considered2
- In fact this test set
is related to the technique called saturation and explained more precisely in [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
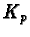 3
3
- Note
that this ordering is well-founded since we have a well-founded ordering
on
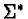 and
and
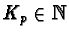 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
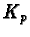 4
4
- Note
that this ordering is well-founded since we have a well-founded ordering
on
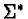 and
and
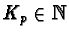 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5
5
- Remember that
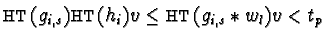 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
6
- If not stated otherwise
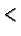 is the usual ordering on
is the usual ordering on 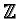 where
where
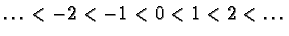 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
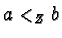 7
7
- Let
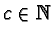 .
We call the positive numbers
.
We call the positive numbers
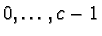 the remainders of
the remainders of 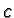 .
Then for each
.
Then for each
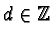 there are unique
there are unique
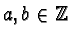 such that
such that
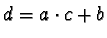 and
and 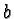 is a remainder of
is a remainder of 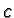 .
We get
.
We get 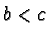 and in case
and in case 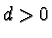 and
and 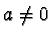 even
even 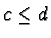 .
Further
.
Further 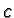 does not divide
does not divide 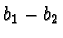 , if
, if 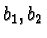 are different remainders of
are different remainders of 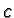 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
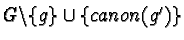 8
8
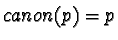 if
if 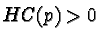 and
and
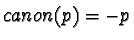 otherwise.
otherwise.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... property9
- By Theorem 6 a set can be characterized as a prefix
Gröbner basis if any element in its right ideal can be prefix reduced to zero using the
set.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.