


Next: Bibliography
Up: Solving One-Sided Equations in
Previous: 4. Conclusions
5. Prefix Gröbner Bases in
![$\mathbb {Z}[{\cal M}]$](img3.gif) and
and
![$\mathbb {Z}[{\cal M}]^k$](img170.gif)
In [3] it was shown how to characterize and compute prefix Gröbner
bases in monoid rings
![$\mathbb {Z}[{\cal M}]$](img3.gif) where
where 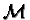 is presented by a finite convergent string
rewriting system.
Here we want to show that if a finite prefix Gröbner basis exists for a right
ideal, then there is also a finite reduced prefix Gröbner basis and we want to list
two important properties of such a basis needed to characterize the solutions of the
homogeneous equations in the previous section.
Further we outline how the technique of Gröbner bases extends to right
is presented by a finite convergent string
rewriting system.
Here we want to show that if a finite prefix Gröbner basis exists for a right
ideal, then there is also a finite reduced prefix Gröbner basis and we want to list
two important properties of such a basis needed to characterize the solutions of the
homogeneous equations in the previous section.
Further we outline how the technique of Gröbner bases extends to right
![$\mathbb {Z}[{\cal M}]$](img3.gif) -modules
-modules
![$\mathbb {Z}[{\cal M}]^k$](img170.gif) .
.
In order to use elements of
![$\mathbb {Z}[{\cal M}]$](img3.gif) as rules for reduction we need an ordering
on
as rules for reduction we need an ordering
on 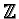 and one on
and one on 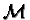 :
We will first specify a total well-founded ordering on
:
We will first specify a total well-founded ordering on 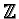 6:
6:
and 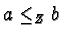 iff
iff 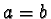 or
or 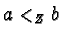 7.
7.
As ordering on 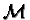 we take the one induced by the completion ordering on
we take the one induced by the completion ordering on 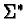 of the string rewriting system.
This ordering has the advantage that it is admissible with respect to concatenation and we have
of the string rewriting system.
This ordering has the advantage that it is admissible with respect to concatenation and we have
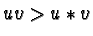 where
where
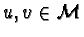 and the multiplication
and the multiplication 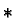 on
on 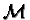 is realized by normal
form computation with respect to the string rewriting system presenting
is realized by normal
form computation with respect to the string rewriting system presenting 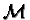 .
.
Then for any
![$p \in \mathbb {Z}[{\cal M}]$](img279.gif) we can characterize its largest term as head term
we can characterize its largest term as head term 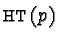 , the
coefficient of this term as
, the
coefficient of this term as 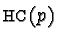 ,
,
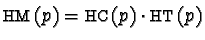 and
and
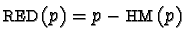 .
.
Let us briefly recall the reduction relation used for
![$\mathbb {Z}[{\cal M}]$](img3.gif) in [3].
in [3].
Prefix Gröbner bases with respect to this reduction relation then can be characterized using the concept of
prefix s-polynomials combined with some extra polynomials which are necessary to describe the
whole right ideal congruence by prefix reduction.
Definition 5
Given two polynomials
![$p_{1}, p_{2} \in \mathbb {Z}[{\cal M}]$](img298.gif)
with
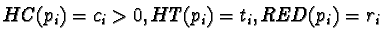
for
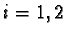
.
If there is
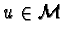
with
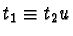
we have to distinguish:
- If
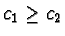 ,
,
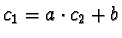 , where
, where
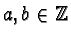 ,
,
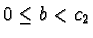 , we get
the following superposition causing a critical pair:
This gives us the prefix s-polynomial
, we get
the following superposition causing a critical pair:
This gives us the prefix s-polynomial
- If
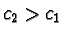 ,
,
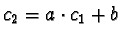 , where
, where
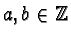 ,
, 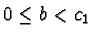 , we get
the following superposition causing a critical pair:
This gives us the prefix s-polynomial
, we get
the following superposition causing a critical pair:
This gives us the prefix s-polynomial
Prefix Gröbner bases then can be characterized by the following theorem from [6]:
The set 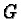 then is called a prefix Gröbner basis of the right ideal it generates.
Notice that without loss of generality we can always assume that all head coefficients
of its polynomials are greater than zero.
then is called a prefix Gröbner basis of the right ideal it generates.
Notice that without loss of generality we can always assume that all head coefficients
of its polynomials are greater than zero.
Lemma 7
Let
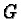
be a finite prefix Gröbner basis and
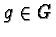
such that
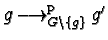
.
Then
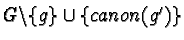 8
8 is again a prefix Gröbner basis
of the same right ideal.
Proof :
1.1
This follows as
![$\mathbb {Z}[{\cal M}]$](img3.gif) can be shown to be a ring with a reduction relation
fulfilling the axioms (A1) - (A4) for reduction rings as presented in [4].
It is easy to see that the reduction relation is terminating (A1), preserves the right
ideal congruence (A2) and for any non-zero polynomial
can be shown to be a ring with a reduction relation
fulfilling the axioms (A1) - (A4) for reduction rings as presented in [4].
It is easy to see that the reduction relation is terminating (A1), preserves the right
ideal congruence (A2) and for any non-zero polynomial
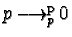 holds (A3).
The important axiom allowing to reduce prefix Gröbner bases without losing the
prefix Gröbner basis property9(A4) holds if for any
holds (A3).
The important axiom allowing to reduce prefix Gröbner bases without losing the
prefix Gröbner basis property9(A4) holds if for any
![$h,p,f,q \in \mathbb {Z}[{\cal M}]$](img330.gif) ,
,
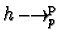 and
and
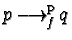 imply
imply
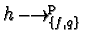 .
.
Let
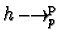 at some monomial
at some monomial 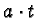 , i.e.
, i.e.
 for some
for some
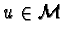 ,
,
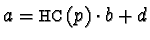 ,
,
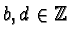 ,
, 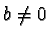 and
and
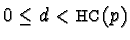 .
Moreover, let
.
Moreover, let
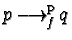 at some monomial
at some monomial 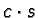 , i.e.
, i.e.
 for some
for some
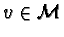 ,
,
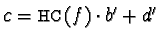 ,
,
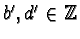 ,
, 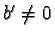 and
and
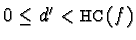 .
We have to distinguish the following cases:
.
We have to distinguish the following cases:
- If
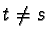 then we are done at once, since
then we are done at once, since
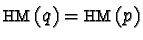 and hence
and hence
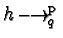 .
.
- If
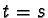 we have to be more careful as
we have to be more careful as
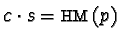 , i.e. the reduction step took place
at the head monomial of
, i.e. the reduction step took place
at the head monomial of 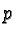 and
and
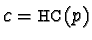 ,
,
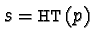 .
.
- If
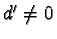 then
then
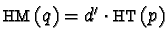 .
We get
.
We get
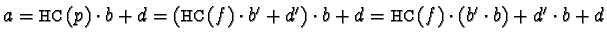 .
Now either
.
Now either
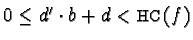 or there exist
or there exist
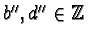 such
that
such
that
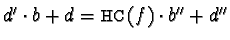 with
with
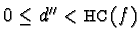 .
In either case
.
In either case 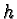 then can be prefix reduced using
then can be prefix reduced using 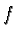 .
.
- If
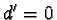 then
then
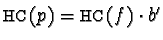 and hence
and hence
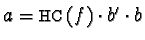 and
and
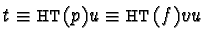 imply that
imply that 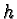 is prefix reducible by
is prefix reducible by 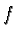 .
.
Now it is easy to see that
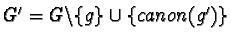 is again a prefix Gröbner basis
of the same right ideal.
If some polynomial
is again a prefix Gröbner basis
of the same right ideal.
If some polynomial
 is reducible by
is reducible by 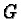 it will also be reducible by
it will also be reducible by 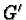 .
q.e.d.
.
q.e.d.
1
Now a prefix Gröbner basis 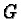 is called reduced if no
is called reduced if no 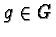 is prefix reducible
by
is prefix reducible
by
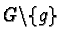 .
.
Lemma 8
Let
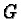
be a reduced prefix Gröbner basis.
Further let
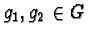
such that
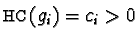
and
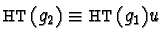
for some
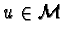
.
Then
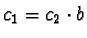
for some
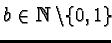
and
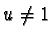
.
Proof :
1.1
We show that the other cases are not possible.
- Assume that
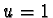 .
.
Then without loss of generality we can also assume 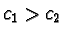 and hence
and hence
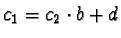 ,
,
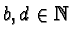 ,
, 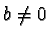 and
and
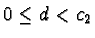 .
Therefore,
.
Therefore,
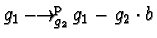 contradicting the
assumption that
contradicting the
assumption that 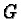 is supposed to be reduced.
is supposed to be reduced.
- Now let
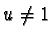 . We have to distinguish two cases:
. We have to distinguish two cases:
- If
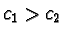 again we have
again we have
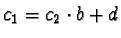 ,
,
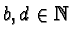 ,
, 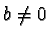 and
and 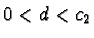 .
This situation now gives rise to an s-polynomial
.
This situation now gives rise to an s-polynomial
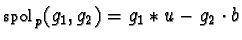 .
Notice that this s-polynomial has head monomial
.
Notice that this s-polynomial has head monomial
 and
hence is neither reducible by
and
hence is neither reducible by 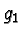 nor by
nor by 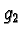 .
On the other hand, as
.
On the other hand, as 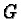 is a prefix Gröbner basis, the s-polynomial must be reducible to zero using
elements of
is a prefix Gröbner basis, the s-polynomial must be reducible to zero using
elements of 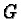 .
Additionally we know that
.
Additionally we know that 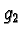 is reducible by this s-polynomial which implies that then
is reducible by this s-polynomial which implies that then
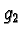 must also be reducible by some element in
must also be reducible by some element in 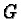 contradicting our assumption of
contradicting our assumption of  being reduced.
being reduced.
- If
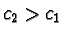 we get
we get
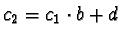 ,
,
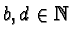 ,
, 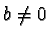 and
and
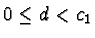 .
Then
.
Then
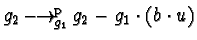 as before contradicting the
assumption that
as before contradicting the
assumption that 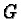 is supposed to be reduced.
is supposed to be reduced.
Hence the only possible case remains to be
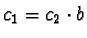 for some
for some
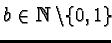 and
and 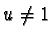 .
As before this gives rise to an s-polynomial, but now we cannot conclude that one of the polynomials
.
As before this gives rise to an s-polynomial, but now we cannot conclude that one of the polynomials 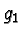 ,
, 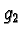 is reducible by it hence since we get no contradiction to
is reducible by it hence since we get no contradiction to 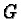 being reduced, this case is possible.
q.e.d.
being reduced, this case is possible.
q.e.d.
1
If we want to compute prefix Gröbner bases of submodules in a right
![$\mathbb {Z}[{\cal M}]$](img3.gif) -module
-module
![$\mathbb {Z}[{\cal M}]^k$](img170.gif) this can be done by introducing a reduction relation and completing it.
Provided a finite basis
this can be done by introducing a reduction relation and completing it.
Provided a finite basis
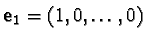 , ...,
, ...,
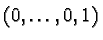 of
of
![$\mathbb {Z}[{\cal M}]^k$](img170.gif) its elements can be represented by polynomials
its elements can be represented by polynomials
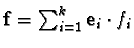 .
A reduction relation now can be defined as follows:
.
A reduction relation now can be defined as follows:
Hence prefix reduction in
![$\mathbb {Z}[{\cal M}]^k$](img170.gif) reduces to prefix reduction in
reduces to prefix reduction in
![$\mathbb {Z}[{\cal M}]$](img3.gif) .
One can show that
.
One can show that
![$\mathbb {Z}[{\cal M}]^k$](img170.gif) together with this reduction relation fulfills (A1) - (A4) for reduction
rings as specified in [4] and Gröbner bases can be characterized using g- and m-polynomials.
The basic idea is to compute a prefix Gröbner basis of a right
together with this reduction relation fulfills (A1) - (A4) for reduction
rings as specified in [4] and Gröbner bases can be characterized using g- and m-polynomials.
The basic idea is to compute a prefix Gröbner basis of a right
![$\mathbb {Z}[{\cal M}]$](img3.gif) -module generated by a set
of vectors
-module generated by a set
of vectors 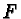 by modifying the set
by modifying the set 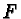 according to the following steps:
according to the following steps:
- initialize a counter
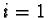 ,
,
- compute a prefix Gröbner basis of the right ideal generated by the head terms
of those vectors
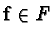 with
with
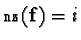 which is in fact a prefix
Gröbner basis computation in
which is in fact a prefix
Gröbner basis computation in
![$\mathbb {Z}[{\cal M}]$](img3.gif) which also affects the components of the vectors involved
``below'' the i-th component,
which also affects the components of the vectors involved
``below'' the i-th component,
- compute a set of solutions for the homogeneous equation related to those vectors
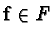 with
with
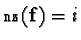 hence generating new generators for the submodule with
non-zero component larger than
hence generating new generators for the submodule with
non-zero component larger than 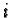 ,
,
- continue for
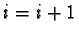 until all components have been handled.
until all components have been handled.



Next: Bibliography
Up: Solving One-Sided Equations in
Previous: 4. Conclusions
| ZCA Home |
Reports |
![]() as rules for reduction we need an ordering
on
as rules for reduction we need an ordering
on ![]() and one on
and one on ![]() :
We will first specify a total well-founded ordering on
:
We will first specify a total well-founded ordering on ![]() 6:
6:
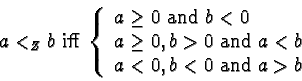
![]() we take the one induced by the completion ordering on
we take the one induced by the completion ordering on ![]() of the string rewriting system.
This ordering has the advantage that it is admissible with respect to concatenation and we have
of the string rewriting system.
This ordering has the advantage that it is admissible with respect to concatenation and we have
![]() where
where
![]() and the multiplication
and the multiplication ![]() on
on ![]() is realized by normal
form computation with respect to the string rewriting system presenting
is realized by normal
form computation with respect to the string rewriting system presenting ![]() .
.
![]() we can characterize its largest term as head term
we can characterize its largest term as head term ![]() , the
coefficient of this term as
, the
coefficient of this term as ![]() ,
,
![]() and
and
![]() .
.
![]() in [3].
in [3].
![]() is called reduced if no
is called reduced if no ![]() is prefix reducible
by
is prefix reducible
by
![]() .
.
![]() -module
-module
![]() this can be done by introducing a reduction relation and completing it.
Provided a finite basis
this can be done by introducing a reduction relation and completing it.
Provided a finite basis
![]() , ...,
, ...,
![]() of
of
![]() its elements can be represented by polynomials
its elements can be represented by polynomials
![]() .
A reduction relation now can be defined as follows:
.
A reduction relation now can be defined as follows: