


Next: 3. The General Case
Up: Solving One-Sided Equations in
Previous: 1. Introduction
2. The Special Case of One Equation
Let
![$f_0, \ldots, f_k \in \mathbb {Z}[{\cal M}]$](img12.gif) and
and
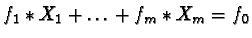 be the equation we want to solve.
In order to describe the generating set of solutions we have to find one solution of
the inhomogeneous equation
be the equation we want to solve.
In order to describe the generating set of solutions we have to find one solution of
the inhomogeneous equation
and if possible a finite set of generators for the solutions of the homogeneous equation
The set of solutions of equation 2 forms a right
![$\mathbb {Z}[{\cal M}]$](img3.gif) -module
-module
![$\mathbb {Z}[{\cal M}]^m$](img17.gif) which is called the right module of syzygies of
which is called the right module of syzygies of
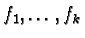 according to the term used for ordinary Gröbner bases in the literature (see e.g. [2]).
To find a generating set for this right module we proceed as suggested in [1]:
according to the term used for ordinary Gröbner bases in the literature (see e.g. [2]).
To find a generating set for this right module we proceed as suggested in [1]:
- Let
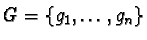 be a finite reduced prefix Gröbner basis of the right ideal
generated by
be a finite reduced prefix Gröbner basis of the right ideal
generated by
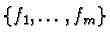 in
in
![$\mathbb {Z}[{\cal M}]$](img3.gif) , and
, and
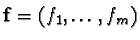 ,
,
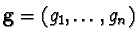 corresponding vectors.
There are two linear mappings given by matrices1
corresponding vectors.
There are two linear mappings given by matrices1
![$P \in {\sf M}_{m \times n}(\mathbb {Z}[{\cal M}])$](img22.gif) ,
,
![$Q \in {\sf M}_{n \times m}(\mathbb {Z}[{\cal M}])$](img23.gif) such that
such that
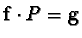 and
and
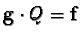 .
.
- Equation 1 is solvable if and only if
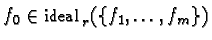 .
This is equivalent to
.
This is equivalent to
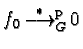 and the reduction sequence gives
rise to a representation
and the reduction sequence gives
rise to a representation
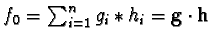 where
where
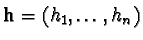 .
Then, as
.
Then, as
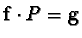 , we get
, we get
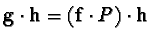 and
and
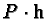 is such a solution of equation 1.
is such a solution of equation 1.
- Let
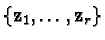 be a generating set for the solutions of the
homogeneous equation
be a generating set for the solutions of the
homogeneous equation
and let 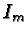 be the
be the 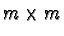 identity matrix.
Further let
identity matrix.
Further let
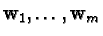 be the columns of the matrix
be the columns of the matrix
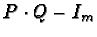 .
Since
.
Since
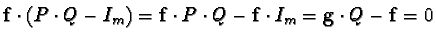 these are solutions of the homogeneous equation 2 as well.
We can even show that the set
these are solutions of the homogeneous equation 2 as well.
We can even show that the set
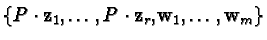 generates all solutions of 2:
generates all solutions of 2:
Let
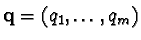 be an arbitrary solution of equation 2,
i.e.
be an arbitrary solution of equation 2,
i.e.
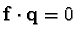 .
Then
.
Then
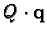 is a solution of equation 3 as
is a solution of equation 3 as
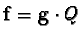 .
Hence there are
.
Hence there are
![$h_1, \ldots, h_r \in \mathbb {Z}[{\cal M}]$](img44.gif) such that
such that
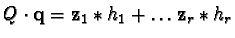 .
Further we find
.
Further we find
and hence 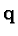 is a right linear combination of elements in
is a right linear combination of elements in
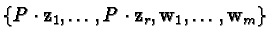 .
.
Now the important part is to find a generating set for the solutions of the homogeneous
equation 3.
Let
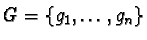 be a finite reduced prefix Gröbner basis of the
right ideal generated by
be a finite reduced prefix Gröbner basis of the
right ideal generated by
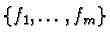 and let
and let
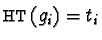 ,
,
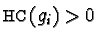 for
for
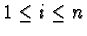 .
In [1] the following situations define a set of generating zeros:
.
In [1] the following situations define a set of generating zeros:
For every 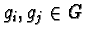 such that
such that 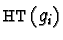 is a prefix (as a word) of
is a prefix (as a word) of 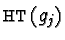 ,
i.e.
,
i.e.
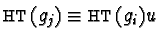 for some
for some
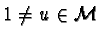 , by Lemma 8 (see Section 5)
we know
, by Lemma 8 (see Section 5)
we know
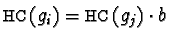 for some
for some
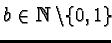 .
We determine vectors
.
We determine vectors 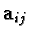 as follows:
as follows:
where the polynomials
![$h_l \in \mathbb {Z}[{\cal M}]$](img64.gif) are due to the reduction sequence
are due to the reduction sequence
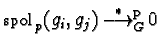 .
.
Then
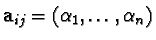 , where
, where
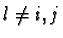 , is a solution of 3 as
, is a solution of 3 as
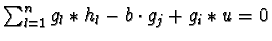 .
.
If no such polynomials exist in 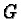 , Baader concluded that the homogeneous equation 3
in the free monoid ring had no solution.
This is no longer true for arbitrary monoid rings.
, Baader concluded that the homogeneous equation 3
in the free monoid ring had no solution.
This is no longer true for arbitrary monoid rings.
Example 1
Let
![$\mathbb {Z}[{\cal M}]$](img3.gif)
be a monoid ring where
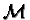
is presented by the string rewriting system
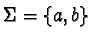
,
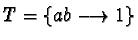
.
Then for the homogeneous equation
we find that the set
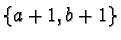
is a reduced prefix Gröbner basis of the right ideal it
generates.
Moreover neither of the head terms of the polynomials in this basis is prefix of the other.
Still the equation can be solved:
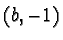
is a solution since
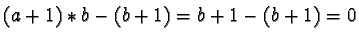
.
This phenomenon is due to the fact that in most monoid rings s-polynomials are not sufficient
for a Gröbner basis test.
In [6] such a test for monoid rings as described here is presented.
Besides testing s-polynomials the following test set has to be considered2:
For
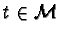 let
let
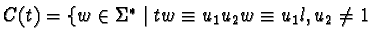 for some
for some
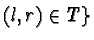 .
Additionally, we define vectors
.
Additionally, we define vectors
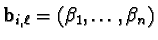 for
for 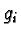 and
and
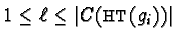 as follows:
Let
as follows:
Let
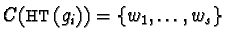 .
For every
.
For every
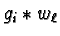 we know
we know
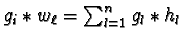 as
as 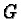 is a prefix Gröbner basis.
Then
is a prefix Gröbner basis.
Then
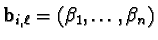 , where
, where
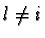 , is a solution of equation 3
as
, is a solution of equation 3
as
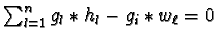 .
.
Lemma 2
The finitely many vectors
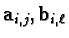
,
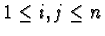
,
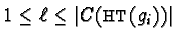
form a right generating set for all solutions of equation
3.
Proof :
1.1
Let
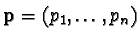 be an arbitrary (non-trivial) solution of 3.
Let
be an arbitrary (non-trivial) solution of 3.
Let
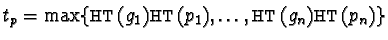 be the maximal term when concatenating the head terms of the multiples in the sum
be the maximal term when concatenating the head terms of the multiples in the sum
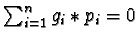 and
and 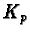 the number of multiples
the number of multiples 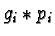 with
with
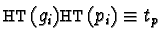 .
A solution
.
A solution 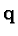 is called smaller than
is called smaller than 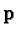 if either
if either 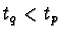 or
or 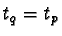 and
and
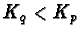 .
We will prove our claim by induction on
.
We will prove our claim by induction on 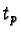 and
and 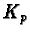 3.
Since we assume
3.
Since we assume 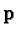 to be a non-trivial solution, we know
to be a non-trivial solution, we know 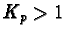 .
Then we can distinguish two cases:
.
Then we can distinguish two cases:
- If there is
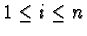 such that
such that
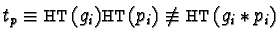 ,
then
,
then
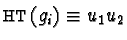 ,
,
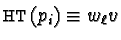 ,
,
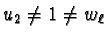 and
and
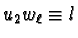 for some
for some
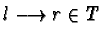 ,
,
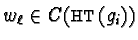 .
Then
.
Then
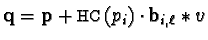 with
with
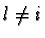 , is again a solution of 3.
It remains to show that it is a smaller one.
To see this we have to examine the multiples
, is again a solution of 3.
It remains to show that it is a smaller one.
To see this we have to examine the multiples 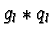 for all
for all
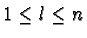 .
Remember that since
.
Remember that since
 we get
we get
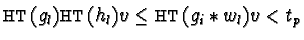 as the
as the 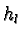 arise from
the reduction sequence
arise from
the reduction sequence
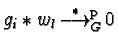 .
.
- For
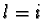 we get
we get
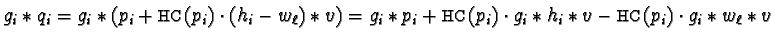 and as
and as
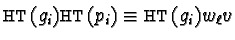 and the resulting monomials
add up to zero we get
and the resulting monomials
add up to zero we get
 .
.
- For
 we get
we get
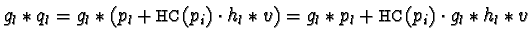 and either
and either
 if
if
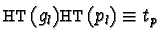 or else
or else
 .
.
Hence either 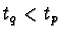 or
or 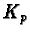 is decreased.
is decreased.
- Let us now assume there are
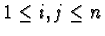 such that
such that
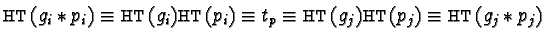 .
Without loss of generality we can assume that
.
Without loss of generality we can assume that
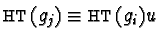 for some
for some
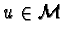 .
Then by Lemma 8 we know that
.
Then by Lemma 8 we know that
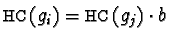 for some
for some
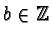 .
For the corresponding s-polynomial
.
For the corresponding s-polynomial
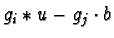 we have a vector
we have a vector 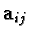 and we can define
and we can define
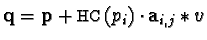 where
where
 with
with
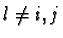 .
It remains to show that this solution indeed is smaller.
To do this we examine the multiples
.
It remains to show that this solution indeed is smaller.
To do this we examine the multiples 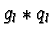 for all
for all
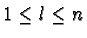 .
.
- For
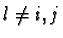 we get
we get
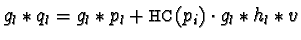 and by Lemma 8
and by Lemma 8
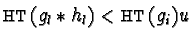 .
Hence
.
Hence
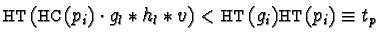 implying either
implying either
 if
if
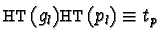 or else
or else
 .
.
- For
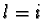 we get
we get
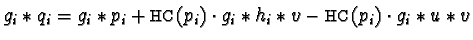 .
Since
.
Since
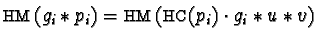 we find
we find
 .
.
- For
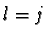 we get
we get
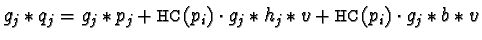 .
Hence either
.
Hence either
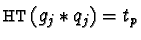 if
if
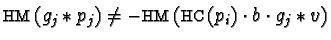 or
or
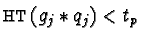 .
.
Hence we find that either 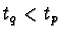 or in case
or in case 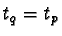 ,
, 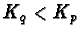 .
Therefore, in all cases the solution
.
Therefore, in all cases the solution 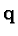 derived from
derived from 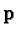 is smaller
and we can show our claim by induction.
is smaller
and we can show our claim by induction.



Next: 3. The General Case
Up: Solving One-Sided Equations in
Previous: 1. Introduction
| ZCA Home |
Reports |
![]() such that
such that ![]() is a prefix (as a word) of
is a prefix (as a word) of ![]() ,
i.e.
,
i.e.
![]() for some
for some
![]() , by Lemma 8 (see Section 5)
we know
, by Lemma 8 (see Section 5)
we know
![]() for some
for some
![]() .
We determine vectors
.
We determine vectors ![]() as follows:
as follows:
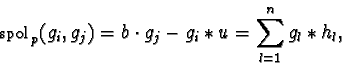
![]() , Baader concluded that the homogeneous equation 3
in the free monoid ring had no solution.
This is no longer true for arbitrary monoid rings.
, Baader concluded that the homogeneous equation 3
in the free monoid ring had no solution.
This is no longer true for arbitrary monoid rings.
![]() let
let
![]() for some
for some
![]() .
Additionally, we define vectors
.
Additionally, we define vectors
![]() for
for ![]() and
and
![]() as follows:
Let
as follows:
Let
![]() .
For every
.
For every
![]() we know
we know
![]() as
as ![]() is a prefix Gröbner basis.
Then
is a prefix Gröbner basis.
Then
![]() , where
, where